かがくのつまみ食い
― 美しい曲線 トロコイド曲線の世界 ―

|

|
Date: 2022/01/11
Title: 美しい曲線 トロコイド曲線の世界(その1)
Category: 数学
Keywords: トロコイド
ネットで面白い記事はないかと探していたら、次の記事を見つけた。それは、ブルーバックスのWebサイトにある連載記事で、
『【数学間違い探し】円の周りを半径が半分の円が一周したら、小さい円は2回転?』
というものだ。
問題の内容は、
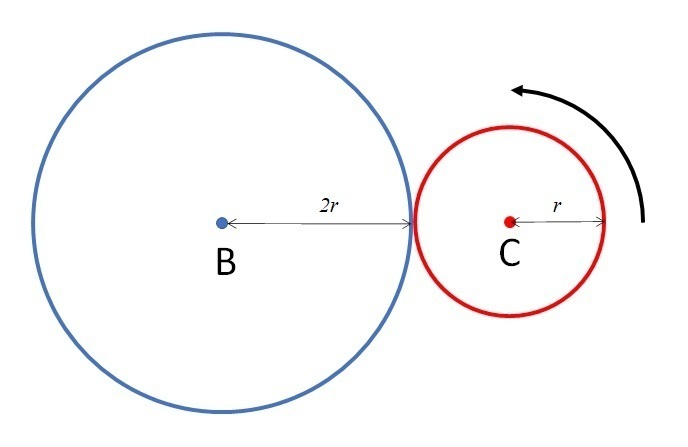
「円Bの半径は円Cの半径の2倍で、円周と円周は外接している。いま、円Bは固定する。そして円Bの周りを、円Cを外接した状態ですべることなくちょうど1周させると、その間に円Cは何回転するかという問題がある。A君は次のように考えた。
A君の考え:半径が2倍ならば、円周も2倍である。そこで、円Bの周りを、円Cを外接した状態ですべることなくちょうど1周させると、その間に円Cは2回転することになる。
A君の考えが正しければ「正しい」と答え、間違っていれば正しい答えを述べなさい。」
というものだ。これはよく知られた問題で、トロコイドに関する初歩的な問題だ。
問題の答えを先にいうと、答えは「3回転」なので、A君の答えは間違っている。
では、なぜA君は間違えたのか?
それは、円Cが円Bの”円周上”を滑らずに回転していることが”ミソ”なのだ。問題が円Bの円周上ではなくて、円Bの円周と同じ長さの”直線上”を円Cが滑らずに回転する場合なら、答えは2回転でA君は正解できたのだが…。
それでは、トロコイドとはどういうものかというと、「円をある曲線(または直線)に沿って滑らないように転がしたとき、その円の内部あるいは外部の定点が描く曲線」のことをいうのだが、上記の問題のように、固定した円(円B:定円という)の外側に接したもう一つの円(円C:動円という)が定円の円周に沿って滑らないように回転していった時に、動円の内部あるいは外側の定点(描画点という)が描く曲線は、外トロコイドまたはエピトロコイドと呼ばれる。特に、問題のように動円の円周上の定点が描く曲線は、外サイクロイドまたはエピサイクロイドと呼ばれるのだ。
1. トロコイド曲線
まずは、円を直線に沿って滑らずに回転させる場合を考えてみよう。
回転させる円(動円)の半径を \(r_m\) 、動円の回転角を \(\theta\) 、描画点の半径を \(r_d\) としたとき、トロコイド曲線を表す座標 は次のように表される(このような表示方法を媒介変数表示という。この場合の媒介変数は動円の回転角 \(\theta\) だ)。
\begin{cases}
x=r_m\theta-r_d\sin\theta \\
y=r_m-r_d\cos\theta
\end{cases}
具体的に \(r_m = 1, r_d = 0.5\) の場合の曲線を描いてみよう。図1-1のように半径 \(r_m = 1\) の円(動円:水色の円)が \(x\) 軸に沿って滑らないように1回転するとき、半径 \(r_d = 0.5\) の円(ピンクの点線の円)上の点(赤い点:描画点)が描く曲線(緑の曲線)が \(r_m = 1, r_d = 0.5\) の場合のトロコイド曲線だ。2つの円の中心は黒い点線 \(y = 1\) に沿って動いていく。また、\(r_m > r_d\) なので、トロコイド曲線は \(x\) 軸と交わることはなく、直線 \(y = 1\) を中心に \(\pm r_d\) の範囲で波打った曲線となる。
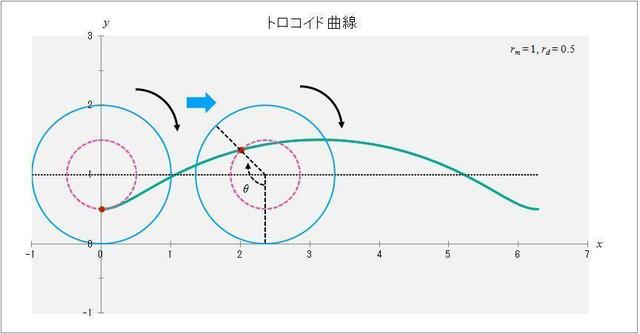
図1-1 \(r_m = 1,\, r_d = 0.5\) の場合のトロコイド曲線が描かれる様子を表した概略図
このことを頭に置いて、\(r_m = 1,\, r_d = 0.2,\, 0.5,\, 1,\, 2,\, 3\) の場合の曲線を \(-2\pi \leqq \theta < 2\pi\) の範囲で描くと図1-2のようになる。
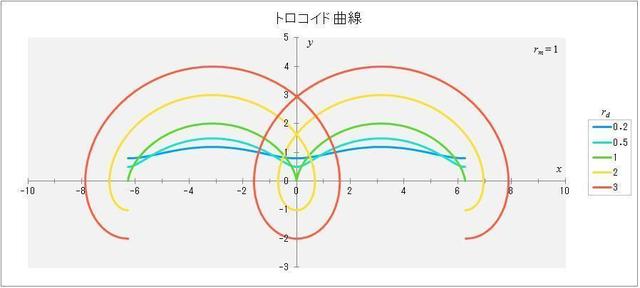
図1-2 \(r_m = 1,\, r_d = 0.2,\,0.5,\,1,\,2,\,3\) の場合のトロコイド曲線
図からもわかるように、\(r_m > r_d\) のときは \(x\) 軸とは交わらず、\(r_m < r_d\) のときは1回の回転で \(x\) 軸と2回交わる。特に、\(r_m = r_d\) のとき、動円上に描画点があるので、1回の回転で \(x\) 軸と1回接することになる。この場合の曲線はサイクロイド(cycloid)と呼ばれるのだ(上の図の緑の曲線)。そして、サイクロイドの式は次のように表される。
\begin{cases}
x=r_m(\theta-\sin\theta) \\
y=r_m(1-\cos\theta)
\end{cases}
具体的に、\(r_m = r_d = 1\) の場合のサイクロイド曲線が描かれる様子を描くと図1-3のようになる。図は動円が原点から1回転したときに描くサイクロイド曲線を表している。
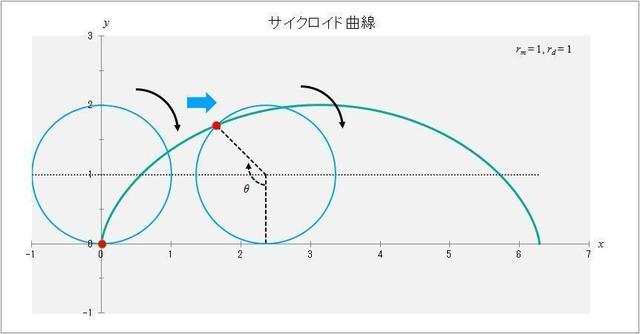
図1-3 \(r_m = r_d = 1\) の場合のサイクロイド曲線が描かれる様子の概略図
ここまでは円を直線に沿って滑らずに回転させる場合について書いてきたが、次回は本題の外トロコイドについて書いてみたい。
関連記事はこちら。
【数学間違い探し】円の周りを半径が半分の円が一周したら、小さい円は2回転?:
https://gendai.ismedia.jp/articles/-/85462?imp=0
Date: 2022/01/1520220115
Title: 美しい曲線 トロコイド曲線の世界(その2)- 外トロコイド
Category: 数学
Keywords: 外トロコイド
2.1 外トロコイドの概要
前回は動円が \(x\) 軸に沿って回転していった場合を考えた。ただ、これだけでは面白くないので、次に半径 \(r_c\) の円(これを定円という)の円周に沿って、円周に外接した半径 \(r_m\) の動円が滑らずに回転する場合を考えてみよう。動円の中心の原点周りの回転角を \(\theta\)、描画点の半径を \(r_d\) としたとき、トロコイド曲線を表す式は次のようになる。これも媒介変数 \(\theta\) で表した式だ。
\begin{cases}
x=\left(r_c+r_m\right)\cos\theta-r_d\cos\left(\frac{r_c+r_m}{r_m}\theta\right) \\
y=\left(r_c+r_m\right)\sin\theta-r_d\sin\left(\frac{r_c+r_m}{r_m}\theta\right)
\end{cases}
そして、この式で表されるトロコイド曲線を外トロコイドまたはエピトロコイドというのだ。特に \(r_m = r_d\) のときは外サイクロイドというのだ。
それでは、具体的に \(r_c = 3,\,r_m = 1,\,r_d = 0.5\) の場合を考えてみよう(図2-1)。
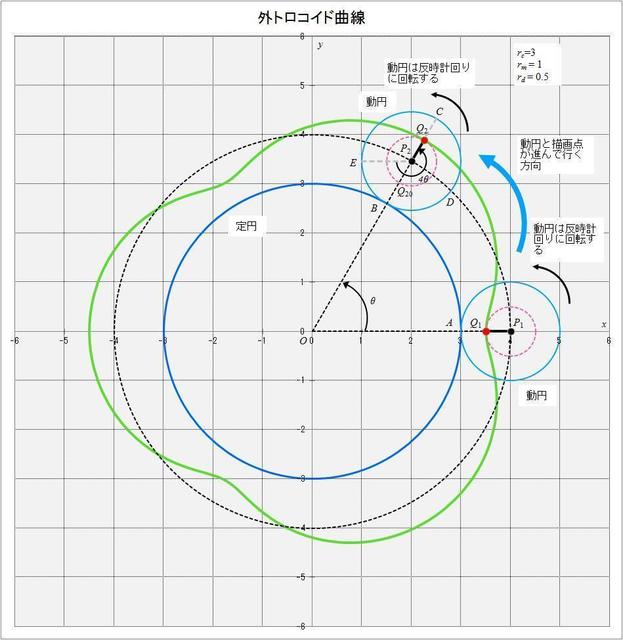
図2-1 \(r_c = 3,\,r_m = 1,\,r_d = 0.5\) の場合の外トロコイド曲線が描かれる様子の概略図
この場合の外トロコイド曲線を表す式は
\begin{cases}
x=4\cos\theta-0.5\cos4\theta \\
y=4\sin\theta-0.5\sin4\theta
\end{cases}
となる。そこで、まずは式の前半の部分を見てみよう。
\begin{cases}
x_1=4\cos\theta \\
y_1=4\sin\theta
\end{cases}
これは半径 \(r_c = 3\) の円(図の青い円:定円)に外接した半径 \(r_m = 1\) の動円(図の水色の円)が滑らずに反時計回りに回転していった時、動円の中心が描く円(半径 \(r_c + r_m = 4\))を表している(図の黒点線の円)。描画点(図の赤い点)は動円が回転していくにしたがって、黒点線の周りを行ったり来たりしながら定円の周りを1周する。
次に式の後半を見てみよう。
\begin{cases}
x_2=-0.5\cos4\theta \\
y_2=-0.5\sin4\theta
\end{cases}
これは動円が回転していった場合の、円を描く動円の中心に対する描画点の相対的な位置を表しているが、三角関数の位相(\(4\theta\))からわかるように、動円が定円の周りを回っていくにしたがって、動円自身はその4倍の速さで回転(自転)していくことを示している。つまり、図のように \(x\) 軸上にあった(\(x = 3.5\))描画点が、動円の中心と原点を結ぶ線が \(x\) 軸となす角が \(\theta\) となったとき、外トロコイド曲線を表す式の後半部分から、動円は \(4\theta\) だけ回転していることになる。これは恒星の周りを惑星が自転しながら公転していく様子をイメージするとわかりやすい。定円の中心に恒星があり、自転しながら定円の周りを回っている動円を惑星と考えると、動円の中心の動きが惑星の公転に相当し、公転速度に対して、惑星は公転速度の4倍の速度で自転しているのだ。
ところで、動円は定円に沿って”滑らずに”回転するので、図のように動円が定円の周りを角 \(\theta\) だけ回ったとき、円弧 AB の長さと円弧 BDC の長さは等しくなる。このときの円弧 BDC の辺 BP2 と辺 CP2 の間の角を \(\phi\) とすると、\(\theta\) と \(\phi\) の関係は次のようになる。
\begin{align}
r_c\theta=r_m\phi
\end{align}
ここで、\(r_c = 3,\,r_m = 1\) なので、
\begin{align}
\phi=\frac{r_c}{r_m}\theta=3\theta
\end{align}
先ほど、動円が定円の周りを \(\theta\) だけ回ったとき、動円はその4倍の 4\(\theta\) 回転していると書いたが、この結果から、動円は 3\(\theta\) しか回転していないのではと思われるかもしれない。前の記事に書いたように定円が直線上を回転する場合は確かにその通りなのだが、今の場合は、動円は定円に沿って滑らずに回転している。定円と動円の半径の比(これはそのまま定円と動円の円周の長さの比となる)と、動円が定円に沿って1周したときの動円の回転数と差はそのために生じているのだ。この点についてもう少し詳しく見てみよう。
回転する前の動円上の点 A は、動円が”同じ面を定円に向けて”定円の周りを \(\theta\) だけ回ったとき、点 A は点 B に移動する。実際には動円は回転しながら移動するので、点 A は点 C に移動する。このとき、\(\angle{\rm BP_2C}\) の角度は \(3\theta\) になることは先ほど述べたとおりだ。
ここで、動円が回転せずに定円の周りを回ったとしたら、点 A は点 E に移動するが、動円は定円に同じ面を向けて定円の周りを回って点 A から点 B に移動するので、この時点で定円は \(\theta\) だけ回転している。これは、月が常に同じ面を地球に向けて公転しているのと同じで、月が地球の周りを \(\theta\) だけ公転したとき、月は同じ角度(\(\theta\))だけ自転している。
したがって、動円が定円の周りを滑らずに回転しながら定円の周りを \(\theta\) だけ回ったとき、動円の回転角は \(\theta + 3\theta = 4\theta\) となるのだ。つまり、動円が回転しながら定円上を1周したとき、動円自体は4回転していることになるのだ。
ここまできたら、前の記事の最初の問題の答えが見えてくる。問題をもう一度書くと、
「円Bの半径は円Cの半径の2倍で、円周と円周は外接している。いま、円Bは固定する。そして円Bの周りを、円Cを外接した状態ですべることなくちょうど1周させると、その間に円Cは何回転するか?」
という問題だ。動円(円C)の半径を \(r_m = 1\) とすると、定円(円B)の半径は \(r_c = 2\) なので、動円が定円の周りを滑らずに角度 \(\theta\) だけ回ると、その間に動円は \(\theta + 2\theta = 3\theta\) だけ回転する。従って動円が定円の周りを滑らずに1周すると、その間に動円は3回転することになる。
話を続けよう。
次に、具体的に \(r_c = 3,\, r_m = 1,\, r_d = 0.5\) の場合に、外トロコイド曲線が描かれていく様子をアニメーションで描くと図2-2のようになる。動円が定円の周りを1周すると動円自信は4回転していることがわかる。
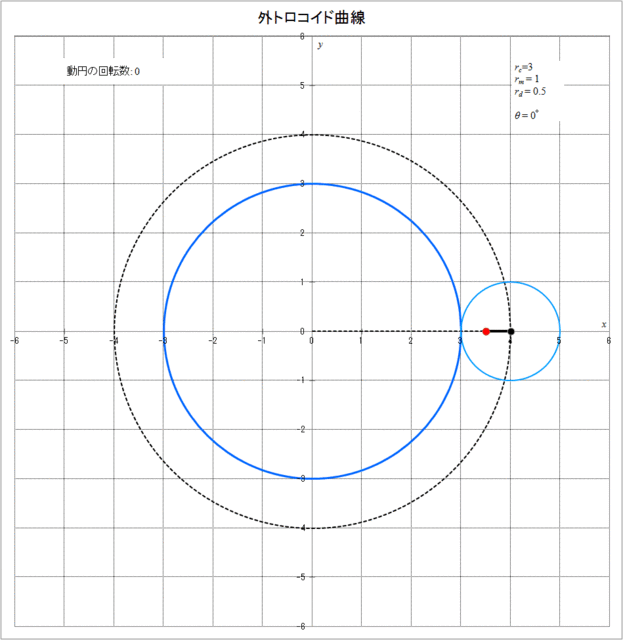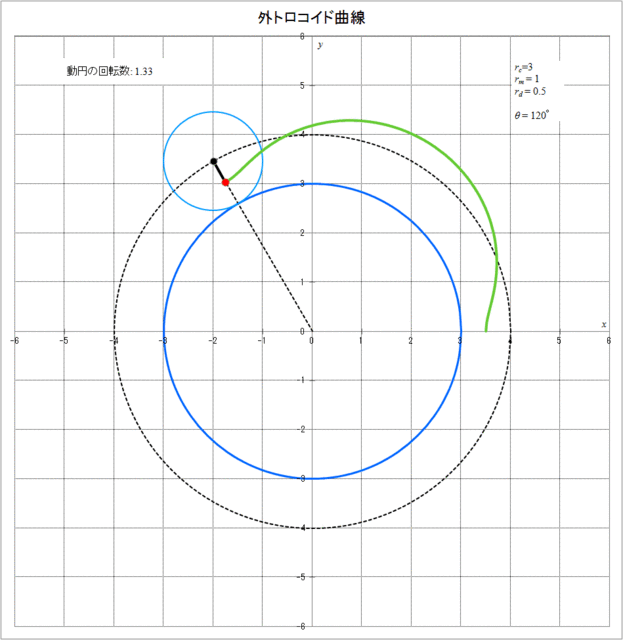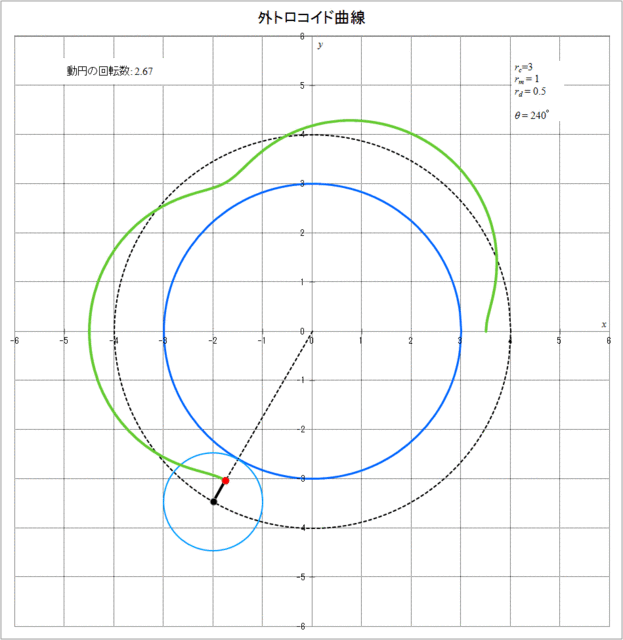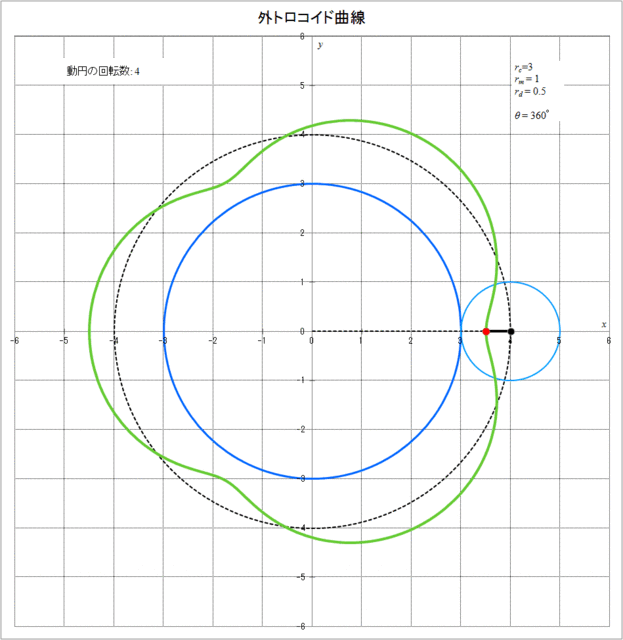
図2-2 外トロコイド曲線が描かれていく様子(\(r_c = 3,\,r_m = 1,\,r_d = 0.5\))
最後に、\(r_c = 3,\,r_m = 1\) で、\(r_d = 0.5,\,1,\,1.5\) の3つの場合の外トロコイド曲線を描くと図2-3のようになる。図からわかるように、
(1) \(r_d = 1\) の場合(図の黄色の曲線)は動円が回転しながら定円上を1周する間に、曲線は3回定円に接することになる。この場合を特に外サイクロイド(またはエピサイクロイド)という。
(2) \(r_d = 1.5\) の場合(図の赤い曲線)は、動円が定円上を1周する間に、定円と6回交わり定円の内側に入り込んだ曲線になる。
(3) \(r_d = 0.5\) の場合(図の緑の曲線)は、曲線は定円とは交わらない。
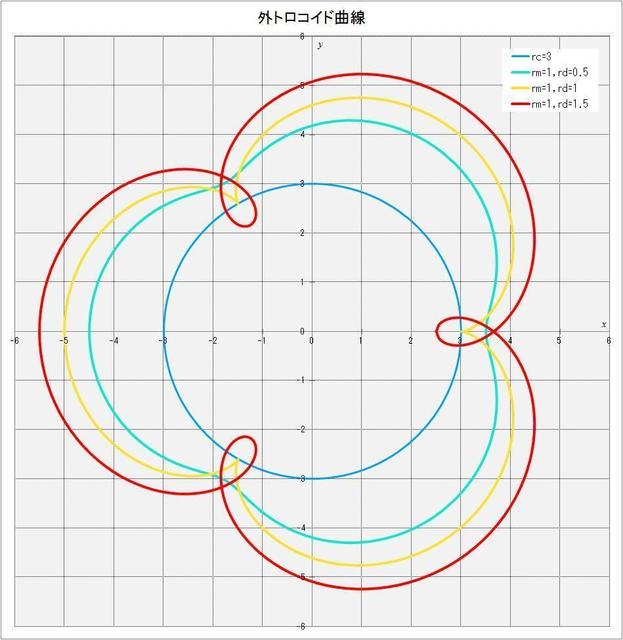
図2-3 \(r_c = 3,\,r_m = 1,\,r_d = 0.5,\,1,\,1.5\) の場合の外トロコイド曲線
ところで、定円と動円の比 \(r_c / r_m\) は一体何を表しているのか?
この比は定円と動円の円周の長さの比なので、動円が定円の周りを1周する間に何回分の外トロコイド曲線を描くか(わかりやすく言えば、上の図の花びらのように膨らんでいる部分が何個あるか)を表しているのだ。図では \(r_c / r_m = 3\) なので、3回分(花びら3個分)の外トロコイド曲線となるのだ。
ここまでは外トロコイドの概略について書いてきたが、次回は外トロコイドの基本形について書いていく。
Date: 2022/01/2620220126
Title: 美しい曲線 トロコイド曲線の世界(その3)- 外トロコイドのつづき
Category: 数学
Keywords: 外トロコイド
2.2 外トロコイド曲線の基本形
これまでは、定円の半径 \(r_c = 3\)、動円の半径 \(r_m = 1\) で、描画点の半径 \(r_d = 0.5,\,1,\,1.5\) という3つの場合について説明してきたが、ここからは定円の半径のみを \(r_c = 3)\) に固定して、\(r_m\) と \(r_d\) をそれぞれ \(r_m =2,\,1.5,\,1,\,0.75,\,0.5\) 、\(r_d = 2,\,1.5,\,1,\,0.75,\,0.5\) とマトリックス状に変えていった場合の外トロコイド曲線の基本形の一部を具体的に示してみよう(下の図2-4)。図では定円 \(r_c\) と動円 \(r_m\) の比 \(r_c/r_m\) も合わせて示してある。
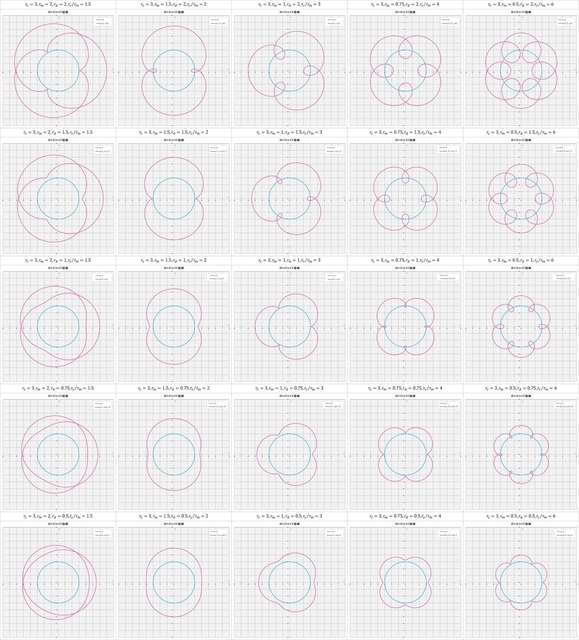
図2-4 \(r_c = 3,\,r_m = 2,\,1.5,\,1,\,0.75,\,0.5,\,r_d = 2,\,1.5,\,1,\,0.75,\,0.5\) の場合の外トロコイド曲線
上の図を見ると、\(r_m\) と \(r_d\) の組み合わせで外トロコイド曲線の規則性が見てとれる。マトリックスの左上から右下にかけての対角の位置にある曲線は、\(r_m = r_d\) なので曲線が定円に接するサイクロイド曲線になっている。それより左下の領域にある曲線は、\(r_m > r_d\) なのでトロコイド曲線は定円には接しない。一方、右上の領域にある曲線は、\(r_m < r_d\) なのでトロコイド曲線は定円の内側にも入り込む。
定円と動円の半径の比 \(r_c/r_m\) の値に応じて、動円が定円の周りを1周したときに描かれる花びらの数が変わるが、\(r_c/r_m = 3/2 = 1.5\) の場合は動円が1周したときは描画点は元の位置に戻っておらず、さらにもう1周した時に初めて元の位置に戻り、3個の花びら描かれる。
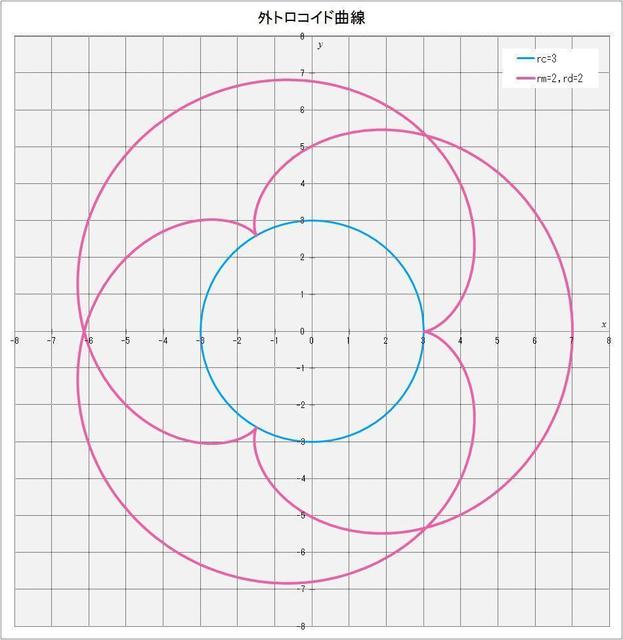
図2-5 \(r_c/r_m = 3/2 = 1.5\) の場合の例(\(r_d = 2\))
これからわかることは、定円と動円の半径の比 \(r_c/r_m\) が \(r_c\)、\(r_m\) がともに最小の整数の比 \(r_c'/r_m'\) で表される場合に、動円は定円の周りを \(r_m'\) 周してはじめて、描画点が元の位置に戻り、\(r_c'\) 個の花びらが描かれるのだ。
もちろん、ここに示したのは外トロコイド曲線の基本形の一部で、\(r_c\)、\(r_m\)、\(r_d\) の組み合わせは無数の存在する。
次からは内トロコイドについて書いていく。
Date: 2022/02/1120220211
Title: 美しい曲線 トロコイド曲線の世界(その4)- 内トロコイド
Category: 数学
Keywords: 内トロコイド
前回は外トロコイドについて書いてきたが、今回からは内トロコイドについて書いていきたいと思う。
3.1 内トロコイドの概要
半径 \(r_c\) の円(定円)の円周に沿って、円周に内接した半径 \(r_m\) の動円が滑らずに回転する場合を考えてみよう。
動円の中心の原点周りの回転角を \(\theta\)、描画点の半径を \(r_d\) としたとき、トロコイド曲線を表す式は次のようになる。この式も媒介変数 \(\theta\) で表した式だ。
\begin{cases}
x=\left(r_c-r_m\right)\cos\theta+r_d\cos\left(\frac{r_c-r_m}{r_m}\theta\right) \\
y=\left(r_c-r_m\right)\sin\theta-r_d\sin\left(\frac{r_c-r_m}{r_m}\theta\right)
\end{cases}
そして、この式で表されるトロコイド曲線を内トロコイドまたはハイポトロコイドといい、特に、\(r_m = r_d\) のときは内サイクロイドという。
それでは、具体的に \(r_c = 5,\,r_m = 3,\,r_d = 5\) の場合を考えてみよう(図3-1)。
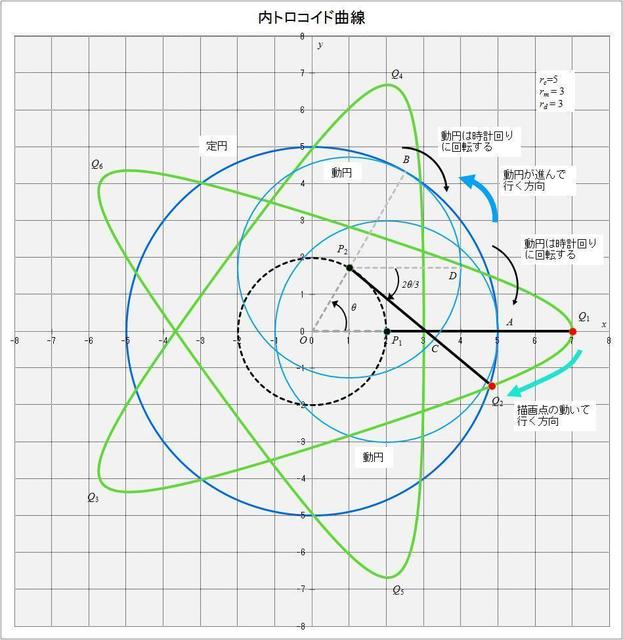
図3-1 \(r_c = 5,\,r_m = 3,\,r_d = 5\) の場合の内トロコイド曲線が描かれる様子の概略図
この場合の内トロコイドの式は以下の通りだ。
\begin{cases}
x=2\cos\theta+5\cos\left(\frac{2}{3}\theta\right) \\
y=2\sin\theta-5\sin\left(\frac{2}{3}\theta\right)
\end{cases}
まずは式の前半の部分を見てみよう。
\begin{cases}
x_1=2\cos\theta \\
y_1=2\sin\theta
\end{cases}
これは半径 \(r_c = 5\) の円(図の青い円:定円)に内接した半径 \(r_m = 3\) の動円(図の水色の円)が滑らずに時計回りに回転していった時、動円の中心が描く円(半径 \(r_c - r_m = 2\))を表している(図の黒点線の円)。
外トロコイドの場合と違ってこの場合の描画点(図の赤い点)の動きは複雑だ。
そこで式の後半を見てみよう。
\begin{cases}
x_2=5\cos\left(\frac{2}{3}\theta\right) \\
y_2=-5\sin\left(\frac{2}{3}\theta\right)
\end{cases}
外トロコイドと同じように、これは動円が回転していった場合の、円を描く動円の中心に対する描画点の相対的な位置を表しているが、三角関数の位相(\(2\theta /3\))からわかるように、動円が定円の周りを回っていくにしたがって、動円自身はその 2/3 倍の速さで回転(自転)していくことを示している。つまり、図のように \(x\) 軸上にあった(\(x = 7\))描画点が、動円と原点を結ぶ線が \(x\) 軸となす角が \(\theta\) となったとき、内トロコイド曲線を表す式の後半部分から、動円は \(2\theta /3\) だけ回転していることになる。
次に、動円は定円に沿って時計回りに回転していくので、動円が回転していった時、描画点の \(y\) 座標は動円の中心に対してマイナス方向に動いていく(これは \(y_2\) の式にマイナスの符号がついていることで表されている)。つまり上の図のように \(x\) 軸上にある動円の中心点が描く円上の点 P1(\(x = 2\))と描画点 Q1(\(x = 7\))は、動円が回転していくにつれてそれぞれ P2、Q2 へと動いていく。そして描画点は図のシアン色の矢印の方向に動いていくのだ(ただし、\(\rm sin\) の値がマイナスとなるような角度領域では描画点の \(y\) 座標は動円の中心に対してプラス方向に動いていく)。
ところで、動円は定円に沿って滑らずに回転するので、図のように動円が定円の周りを角 \(\theta\) だけ回ったとき、円弧 AB の長さと円弧 BC の長さは等しくなる。このときの円弧 BC の辺 BP2 と辺 CP2 の間の角を \(\phi\) とすると、\(\theta\) と \(\phi\) の関係は次のようになる。
\begin{align}
r_c\theta=r_m\phi
\end{align}
ここで、\(r_c = 5,\,r_m = 3\) なので、
\begin{align}
\phi=\frac{r_c}{r_m}\theta=\frac{5}{3}\theta
\end{align}
先ほど、動円が定円の周りを \(\theta\) だけ回ったとき、動円はその 2/3 倍の \(2\theta /3\) 回転していると書いたが、この結果から、動円は時計回りに \(5\theta /3\) だけ回転しているのではと思われるかもしれない。じつは、これも外トロコイドで説明したのと同じ事情によるのだ。
回転する前の動円上の点 A は、動円が同じ面を定円に向けて定円の周りを反時計回りに \(\theta\) だけ回ったとき、点 A は点 B に移動する。実際には動円は時計回りに回転しながら移動するので、点 A は点 C に移動する。このとき、\(\angle\)BP2C の角度は \(5\theta /3\) になることは先ほど述べたとおりだ。
ここで、動円が回転せずに定円の周りを回ったとしたら、点 A は点 D に移動するが、動円は定円に同じ面を向けて定円の周りを回っているので、この時点で動円は反時計回りに \(\theta\) だけ回転している。したがって、動円が定円の周りを滑らずに回転しながら定円の周りを \(\theta\) だけ回ったとき、動円の回転角は \(5\theta /3 - \theta = 2\theta /3\) となるのだ。つまり、動円が回転しながら定円上を反時計回りに 1 周したとき、動円自体は時計回りに 2/3 回転していることになるのだ。
さらに、定円の円周の長さ \(10\pi\) に対して、動円の円周の長さは \(6\pi\) なので、動円が回転しながら定円上を1周したときには、動円は 2/3 回転しかしていなので、描画点は元の位置には戻っていない。描画点が元の位置に戻るためには定円の周りを 3 周する必要がある。定円の円周の長さは \(10\pi\) なので、3 周分の長さ \(30\pi\) だけ動円が動くためには、動円の円周の長さは \(6\pi\) なので、動円の円周の長さの5倍分だけ動く必要がある。そのため描画点が元の位置に戻った時、星型のトロコイド曲線が描かれることになるのだ。
次に、\(r_c = 5\)、\(r_m = 3\) で、\(r_d = 1,\,3,\,5\) の3つの場合の内トロコイド曲線を描くと図3-2のようになる。図からわかるように、
① \(r_d = 3\) の場合(図の黄色の曲線)は動円が回転しながら定円上を3周する間に、曲線は5回定円に接することになるが、\(r_d = 5\) の場合より尖った星型になる。この場合を特に内サイクロイド曲線という。
② \(r_d = 5\) の場合(図の水色の曲線)は、動円が定円上を3周する間に、定円と10回交わり定円の外側にはみ出した曲線になる。
③ \(r_d = 1\) の場合(図の赤い曲線)は曲線は定円とは交わらず、曲線の形も星型というよりは花びらのような形になる。
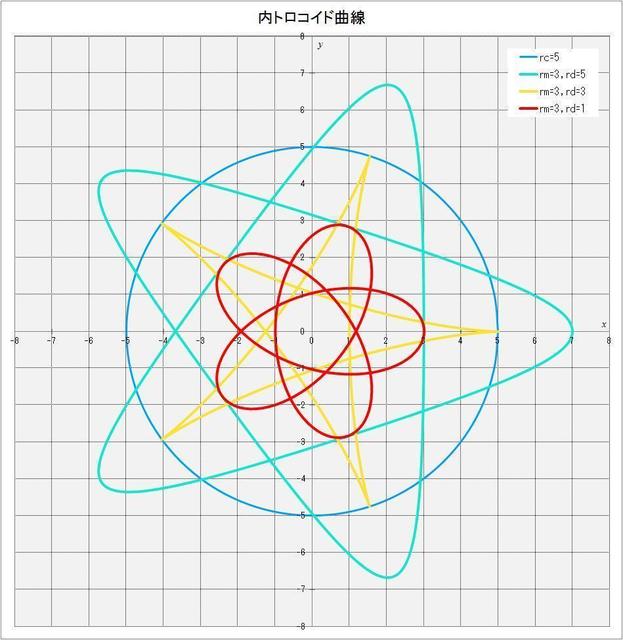
図3-2 \(r_c = 5,\,r_m = 3,\,r_d = 1,\,3,\,5\) の場合の内トロコイド曲線
それでは、具体的に \(r_c = 5,\,r_m = 3,\,r_d = 5\) の場合に、内トロコイド曲線が描かれていく様子をアニメーションで描くと図3-3のようになる。動円が定円の周りを1周(\(\theta = 360^{\circ}\))または2周(\(\theta = 720^{\circ}\))した時点では描画点は最初の位置には戻っておらず、3周(\(\theta = 1080^{\circ}\))して初めて描画点が最初の位置に戻り、その時動円は2回転していることがわかる。
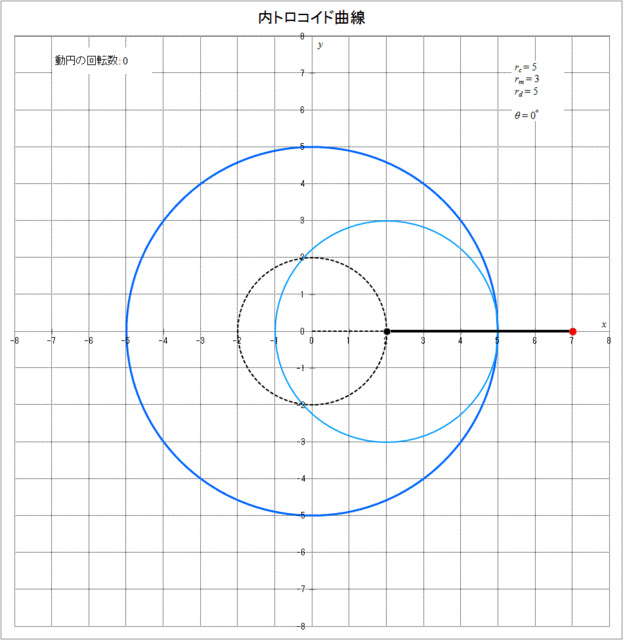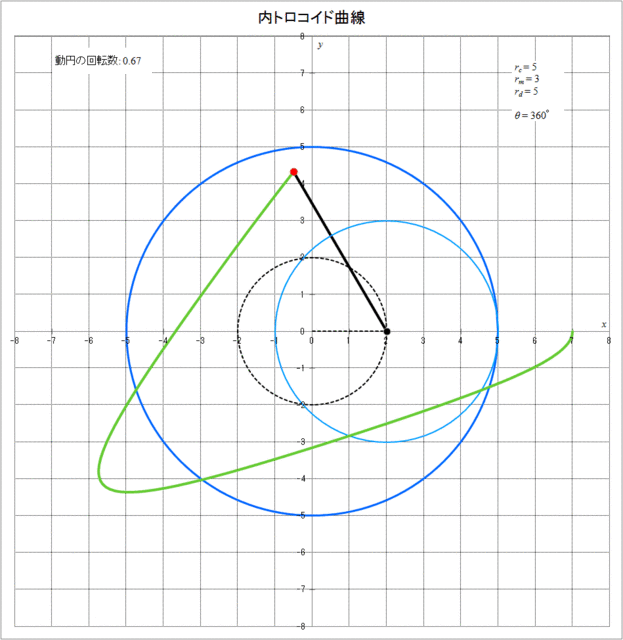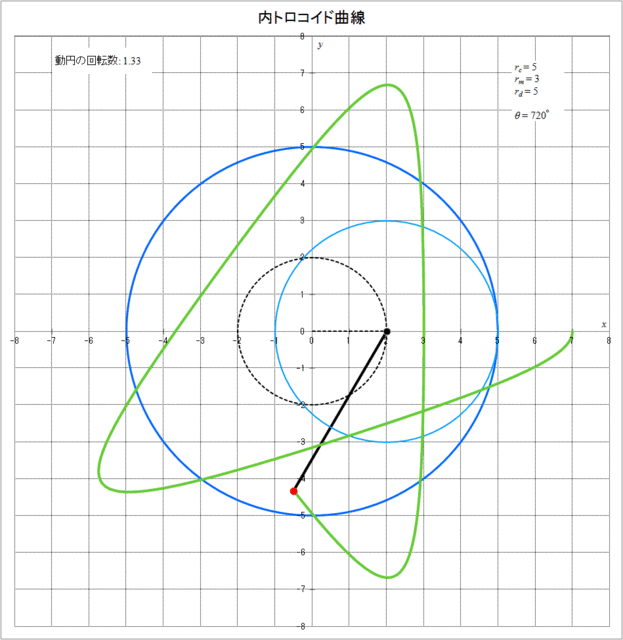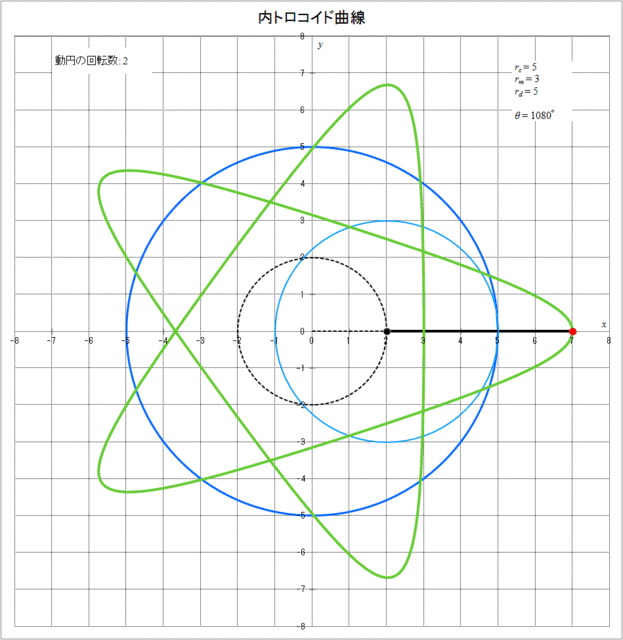
図3-3 内トロコイド曲線が描かれていく様子(\(r_c = 5,\,r_m = 3,\,r_d = 5\))
同様に、\(r_c = 5,\,r_m = 3,\,r_d = 1\) の場合、 内トロコイド曲線が描かれていく様子をアニメーションで描くとと図3-4のようになる。この図から、図3-3と同様に動円が定円の周りを1周(\(\theta = 360^{\circ}\))または2周(\(\theta = 720^{\circ}\))した時点では描画点は最初の位置には戻っておらず、3周(\(\theta = 1080^{\circ}\))して初めて描画点が最初の位置に戻り、その時動円は2回転していることがわかる。しかし、この場合は図3-3とは逆向きに内トロコイド曲線が描かれていくのがわかる。その分かれ目となるのは \(r_m = r_d\) となる場合(内サイクロイド曲線となる場合)で、\(r_m > r_d\) の場合(描画点が動円の内側にある)と \(r_m \leqq r_d\) の場合(描画点が動円上または動円の外側にある)とで内サイクロイド曲線が描かれる方向が逆向きとなる。
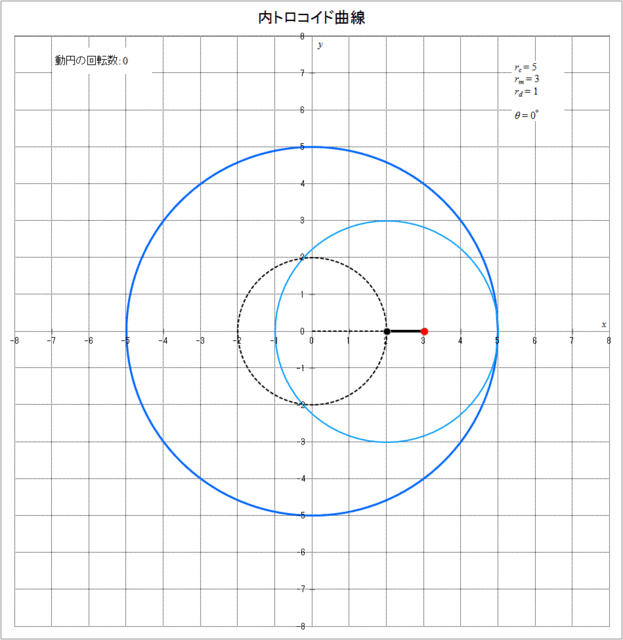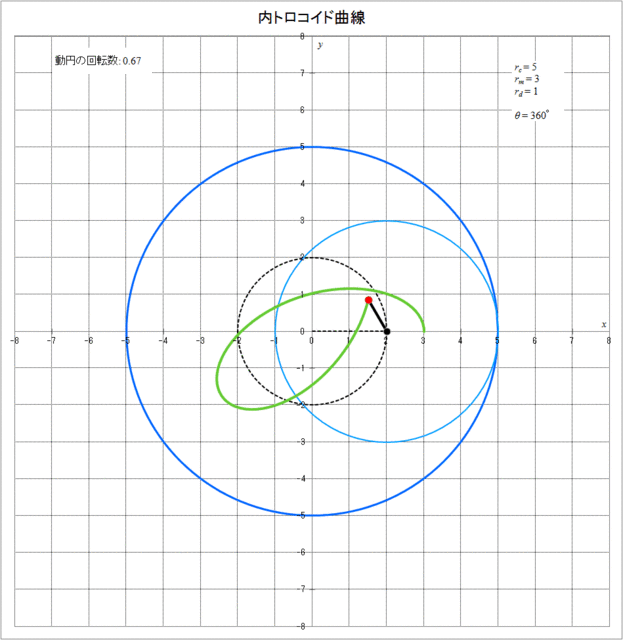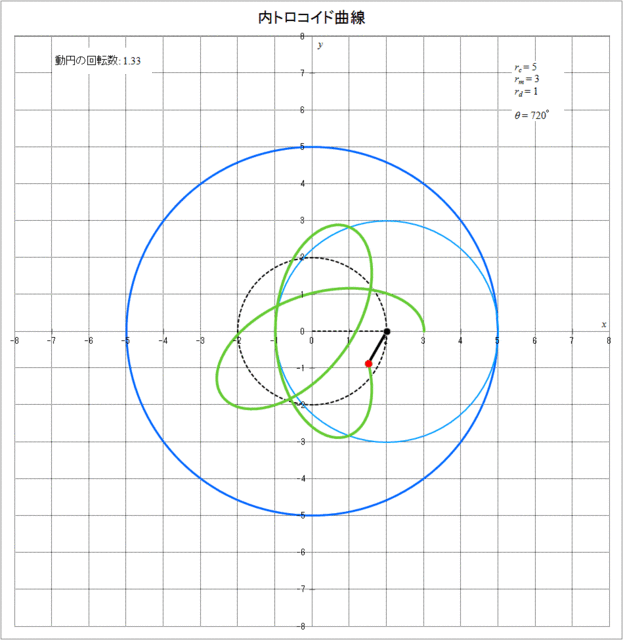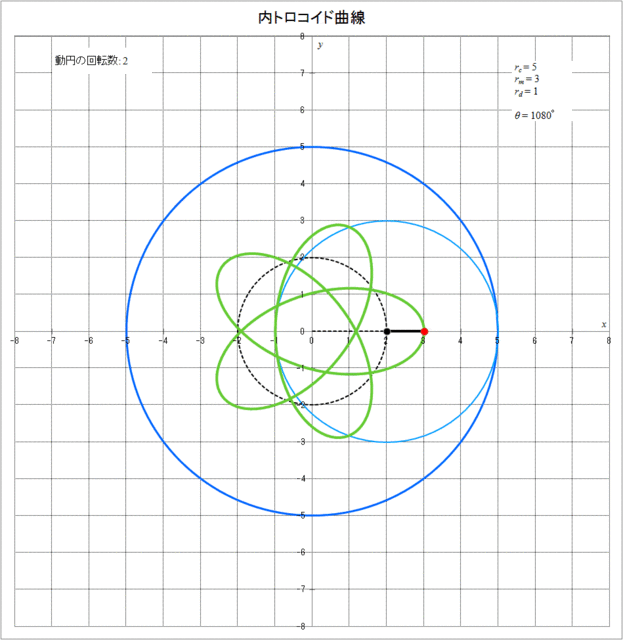
図3-4 内トロコイド曲線が描かれていく様子(\(r_c = 5,\,r_m = 3,\,r_d = 1\))
次は、少し特別な場合について書いていく。
Date: 2022/02/2020220220
Title: 美しい曲線 トロコイド曲線の世界(その5)- 内トロコイド(2)
Category: 数学
Keywords: 内トロコイド
3.2 内トロコイドの概要(2)
前回は内トロコイドの基本形について書いてきたが、ここからは \(r_c = 2r_m\) という特別な場合を考えてみよう。この場合の内トロコイド曲線を表す式は以下のようになる。
\begin{cases}
x=r_m\cos\theta+r_d\cos\theta \\
y=r_m\sin\theta-r_d\sin\theta
\end{cases}
これについて具体的に \(r_c = 5,\,r_m = 2.5,\,r_d = 5\) の場合を考えてみよう(図3-5)。
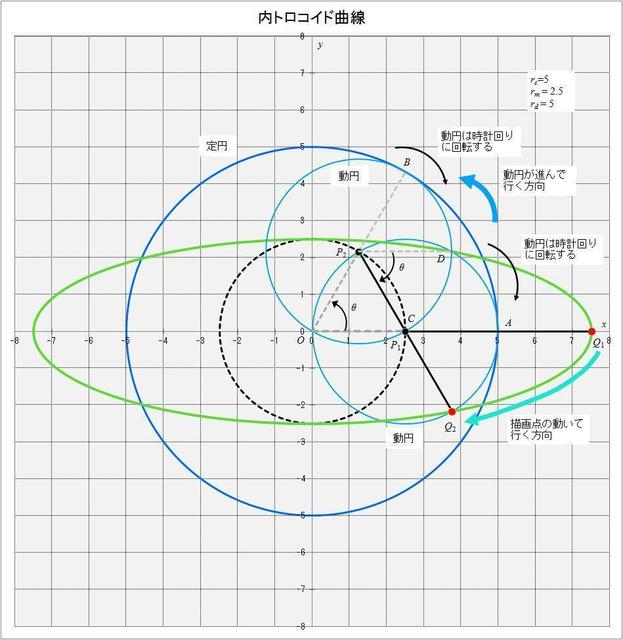
図3-5 \(r_c = 5,\,r_m = 2.5,\,r_d = 5\) の場合の内トロコイド曲線が描かれる様子の概略図
この場合の内トロコイド曲線を表す式は次の通りだ。
\begin{cases}
x=2.5\cos\theta+5\cos\theta \\
y=2.5\sin\theta-5\sin\theta
\end{cases}
まずは式の前半部分を見てみよう。
\begin{cases}
x_1=2.5\cos\theta \\
y_1=2.5\sin\theta
\end{cases}
これまでの説明と同様に、これは半径 \(r_c = 5\) の円(図の青い円:定円)に内接した半径 \(r_m = 2.5\) の動円(図の水色の円)が滑らずに時計回りに回転していった時、動円の中心が描く円(半径 \(r_c - r_m = 2.5\)) を表している(図の黒点線の円)。
次に式の後半部分は
\begin{cases}
x_2=5\cos\theta \\
y_2=-5\sin\theta
\end{cases}
となるが、これまで説明してきたように、これは動円が回転していった場合の、円を描く動円の中心に対する描画点の相対的な位置を表しているが、三角関数の位相部分(\(\theta\))からわかるように、動円が定円の周りを回っていくにしたがって、動円自身は同じ速さで回転していくことを示している。つまり、図のように \(x\) 軸上にあった(\(x = 7.5\))描画点が、動円と原点を結ぶ線が \(x\) 軸となす角が \(\theta\) となったとき、内トロコイド曲線を表す式の後半部分から、動円も \(\theta\) だけ回転していることになる。
次に、動円は定円に沿って時計回りに回転していくので、動円が回転していった時、描画点の \(y\) 座標は動円の中心に対してマイナス方向に動いていく(これは \(y_2\) の式にマイナスの符号がついていることで表されている)。つまり上の図のように \(x\) 軸上にある動円の中心点が描く円上の点 P1(\(x = 2.5\))と描画点 Q1(\(x = 7.5\))は、動円が回転していくにつれてそれぞれ P2、Q2 へと動いていく。そして描画点は図のシアン色の矢印の方向に動いていくのだ(ただし、\(\sin\) の値がマイナスとなるような角度領域では描画点の \(y\) 座標は動円の中心に対してプラス方向に動いていく)。
ところで、動円は定円に沿って滑らずに回転するので、図のように動円が定円の周りを角 \(\theta\) だけ回ったとき、円弧 AB の長さと円弧 BDC の長さは等しくなる。このときの円弧 BDC の辺 BP2 と辺 CP2 の間の角を \(\phi\) とすると、\(\theta\) と \(\phi\) の関係は次のようになる。
\begin{align}
r_c\theta=r_m\phi
\end{align}
ここで、\(r_c = 5,\,r_m = 2.5\) なので、
\begin{align}
\phi=\frac{r_c}{r_m}\theta=2\theta
\end{align}
先ほど、動円が定円の周りを \(\theta\) だけ回ったとき、動円は同じ角度 \(\theta\) だけ回転していると書いたが、この結果から、動円は時計回りに \(2\theta\) だけ回転しているのではと思われるかもしれない。実は、これもこれまで説明してきたのと同じ事情によるのだ。
回転する前の動円上の点 A は、動円が同じ面を定円に向けて定円の周りを反時計回りに \(\theta\) だけ回ったとき、点 A は点 B に移動する。実際には動円は時計回りに回転しながら移動するので、点 A は点 C に移動する。このとき、\(\angle\)BP2C の角度は \(2\theta\) になることは先ほど述べたとおりだ。
ここで、動円が回転せずに定円の周りを回ったとしたら、点 A は点 D に移動するが、動円は定円に同じ面を向けて定円の周りを回っているので、この時点で定円は反時計回りに \(\theta\) だけ回転している。したがって、動円が定円の周りを滑らずに回転しながら定円の周りを \(\theta\) だけ回ったとき、定円の回転角は \(2\theta - \theta = \theta\) となるのだ。つまり、動円が回転しながら定円上を反時計回りに1周したとき、動円自体も時計回りに1回転していることになるのだ。
さらに、定円の円周の長さ \(10\pi\) に対して、動円の円周の長さは \(5\pi\) なので、動円が回転しながら定円上を1周したときには、動円はその円周の2周分を動かなければならない。しかし、動円自体は1回転しかしていなので、描画点が元の位置には戻るためには動円は2回転しなければならないのではと思いたくなる。
実はこれはこういうことだ。
\(\theta = 0^{\circ}\) の時、\(x\) 軸上(\(x = 7.5\))にある描画点は、動円が定円上を半周したとき(\(\theta = 180^{\circ}\))描画点は \(x\) 軸上の正反対の位置にある(\(x = -7.5\))。このとき動円は半回転しかしてないが、この時点で動円は定円に沿って \(5\pi\) だけ動いていて、これは動円の円周の長さに相当する。したがって、動円がさらに定円に沿って半周して( \(5\pi\) 動いて)元の位置に戻ったときには、動円はさらに半回転して最終的に1回転することになる。その結果、楕円形のトロコイド曲線が描かれることになるのだ。
\(r_c = 5,\,r_m = 2.5,\,r_d = 5\) の場合について、内トロコイド曲線が描かれる様子をアニメーションで表したものを図3-6に示す。
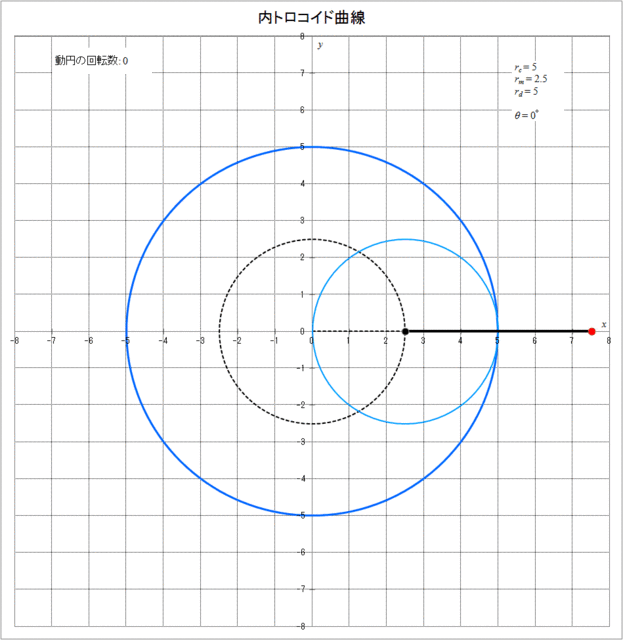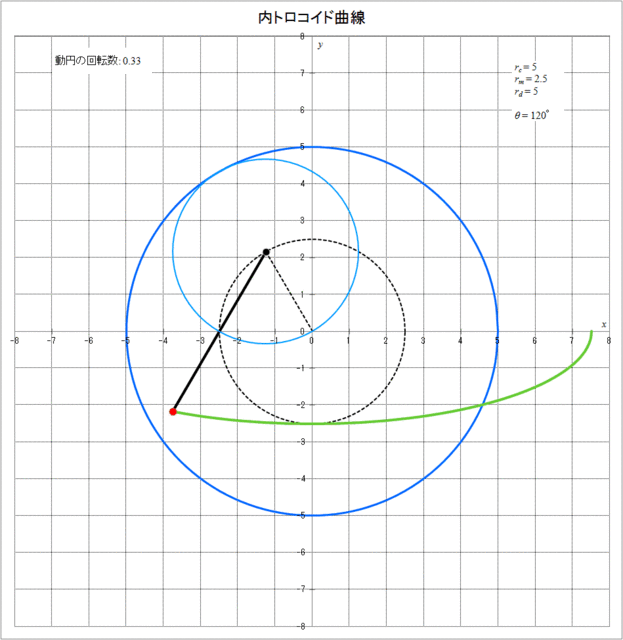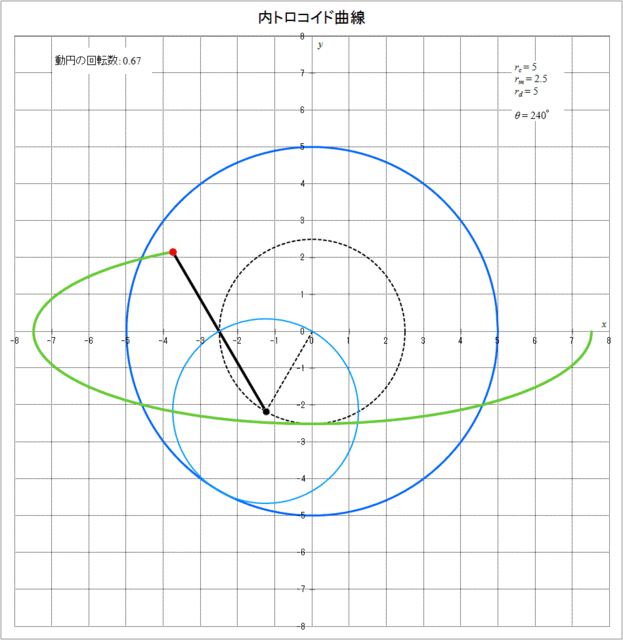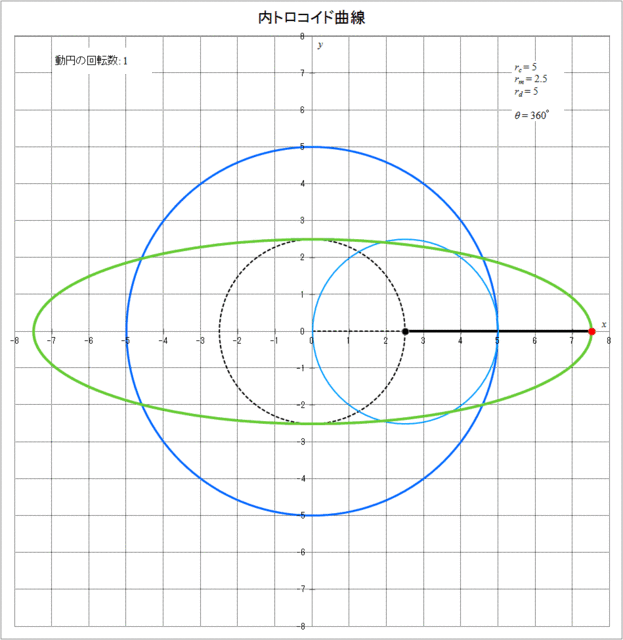
図3-6 内トロコイド曲線が描かれていく様子(\(r_c = 5,\,r_m = 2.5,\,r_d = 5\))
さらにもう一つの場合、\(r_c = 5,\,r_m = 2.5,\,r_d = 1\) の場合も同様に内トロコイド曲線を表す式は
\begin{cases}
x=2.5\cos\theta+\cos\theta \\
y=2.5\sin\theta-\sin\theta
\end{cases}
で、曲線が描かれる様子を描いた概略図は図3-7のようになる。この場合は描画点が動円の内側にあるので、曲線が描かれる向きが \(r_d = 5\) の場合とは逆に反時計回りになることに注意する。
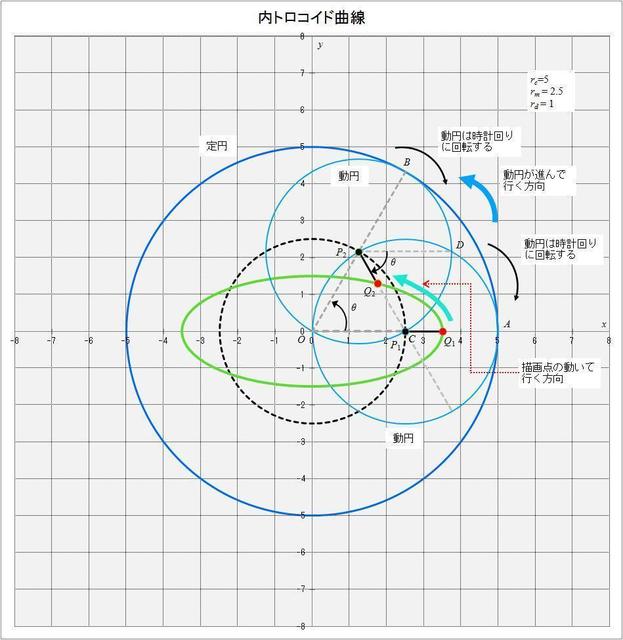
図3-7 \(r_c = 5,\,r_m = 2.5,\,r_d = 1\) の場合の内トロコイド曲線が描かれる様子の概略図
この場合の内トロコイド曲線が描かれる様子をアニメーションにしたものを図3-8に示す。
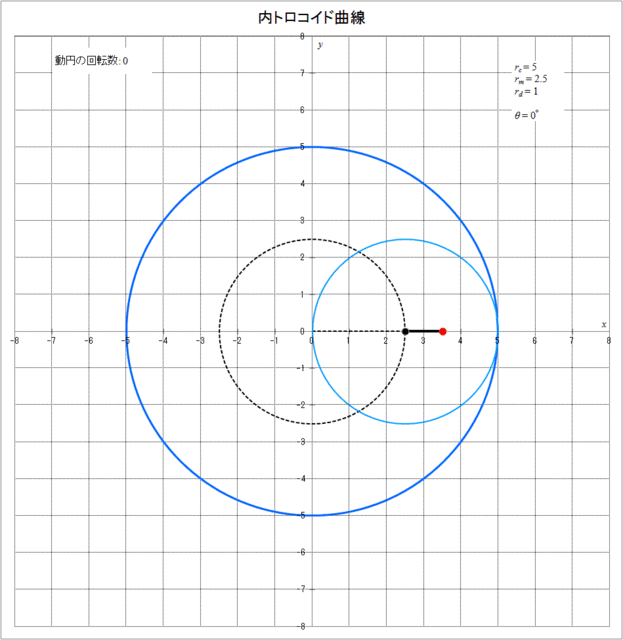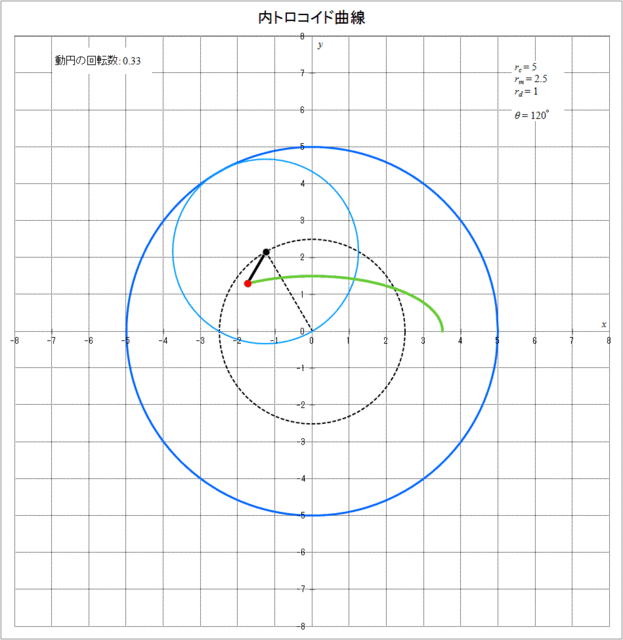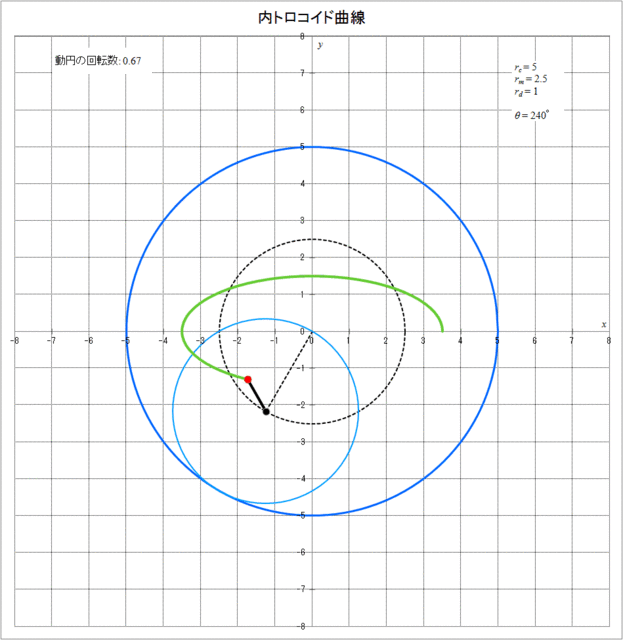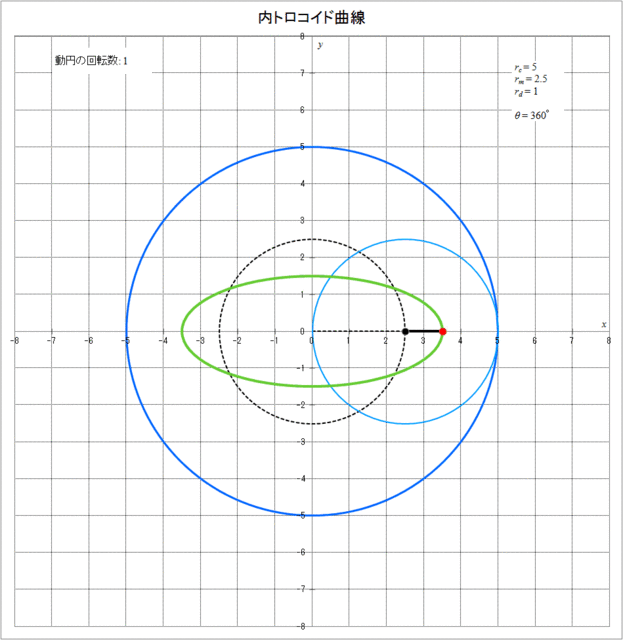
図3-8 内トロコイド曲線が描かれていく様子(\(r_c = 5,\,r_m = 2.5,\,r_d = 1\))
ところで、\(r_m\) と \(r_d\) の比を \(k\) とすると(\(r_m = kr_d\)、ただし \(k>0\))、内トロコイド曲線は次のように表される。
\begin{cases}
x=r_m\cos\theta+r_d\cos\theta=\left(k+1\right)r_d\cos\theta \\
y=r_m\sin\theta-r_d\sin\theta=\left(k-1\right)r_d\sin\theta
\end{cases}
これを変形すると、
\begin{align}
\frac{x}{\left(k+1\right)r_d}=\cos\theta,\quad\frac{y}{\left(k-1\right)r_d}=\sin\theta
\end{align}
となるので、それぞれ2乗して足し合わせると、
\begin{align}
\frac{x^2}{\left[\left(k+1\right)r_d\right]^2}+\frac{y^2}{\left[\left(k-1\right)r_d\right]^2}=\cos^2\theta+\sin^2\theta=1
\end{align}
となる。
ん? これはどこかで見た式だ。そう、これはまさに楕円を表す式だ。楕円の長径を \(a\)、短径を \(b\) とすると、
\begin{align}
a=\left(k+1\right)r_d,\quad b=|\left(k-1\right)r_d|
\end{align}
となる。ここで、短径が絶対値表記になっているのは、\(r_m < r_d\) の場合は \(k-1 < 0\) なので \(b < 0\) となるためだ。
次に、\(r_c = 5,\,r_m = 2.5\) で、\(r_d = 1,\,3,\,5\) の3つの場合の内トロコイド曲線を描くと図3-9のようになる。
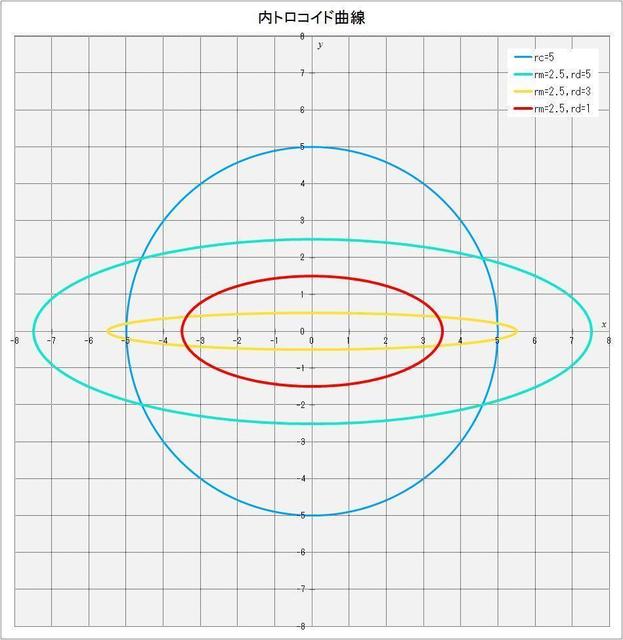
図3-9 \(r_c = 5,\,r_m = 2.5,\,r_d = 1,\,3,\,5\) の場合の内トロコイド曲線
図からわかるように、
① \(r_d = 5\) の場合(図の水色の曲線)は \(k = 0.5\) なので、長径 \(a = 7.5\)、短径 \(b = 2.5\) の楕円で、定円からはみ出した楕円となる。
② \(r_d = 3\) の場合(図の黄色の曲線)は \(k = 0.83\) なので、長径 \(a = 5.5\)、短径 \(b = 0.5\) の楕円で、定円からわずかにはみ出した非常に細長い楕円となる。
③ \(r_d = 1\) の場合(図の赤色の曲線)は \(k = 2.5\) なので、長径 \(a = 3.5\)、短径 \(b = 1.5\) の楕円で、定円の内側にある楕円となる。
また、\(r_m = r_d\) のときは内サイクロイドとなるが、この場合は \(k = 1\) なので、短径 \(b = 0\) となって定円に接した完全に潰れた楕円、つまり直線となる。
楕円の潰れ具合を表す指標として扁平率があるが、これは次の式で表される。
\begin{align}
f=\frac{a-b}{a}
\end{align}
\(r_m < r_d\,(k < 1)\) の場合は
\begin{align}
f=\frac{a-b}{a}=\frac{\left[\left(k+1\right)+\left(k-1\right)\right]r_d}{\left(k+1\right)r_d}=\frac{2k}{k+1}
\end{align}
\(r_m > r_d\,(k > 1)\) の場合は
\begin{align}
f=\frac{a-b}{a}=\frac{\left[\left(k+1\right)-\left(k-1\right)\right]r_d}{\left(k+1\right)r_d}=\frac{2}{k+1}
\end{align}
\(r_m = r_d\,(k = 1)\) の場合は短径 \(b = 0\) なので \(f = 1\) となる。
ところで、内トロコイド曲線が円(\(f = 0\))となることはありうるのか?
上の式から \(f = 0\) となるのは \(k = 0\) または \(k = \infty\) の場合だけだ(ただし、\(k > 0\))。つまり \(k\) の値がだんだん大きくなっていくと円に近づいていくが、完全な円になることはない。
今回は \(r_c = 2r_m\) という特別な場合について書いてきたが、このケースでは内トロコイドは楕円(\(r_m = r_d\) のときは直線)にしかならず、\(r_d\) の値で楕円のつぶれ具合が変わるだけで、美しくもなく、何の変哲もない曲線にしかならない(この記事のタイトルとは矛盾するけど…)。
つづく。
Date: 2022/03/1020220310
Title: 美しい曲線 トロコイド曲線の世界(その6)- 内トロコイド(3)
Category: 数学
Keywords: 内トロコイド
3.3 内トロコイド曲線の基本形
これまでは、\(r_c = 5\) で \(r_m\) と \(r_d\) の値がいくつかの場合について説明してきたが、ここからは定円の半径を \(r_c = 5\) に固定して \(r_m\) と \(r_d\) をそれぞれ \(r_m = 4,\,3,\,2,\,1.5,\,1,\,r_d =4,\,3,\,2,\,1.5,1\) と変えていった場合の内トロコイド曲線の基本形の一部を具体的に示してみよう(図3-10)。図では定円 \(r_c\) と動円 \(r_m\) の比 \(r_c / r_m\) も合わせて示してある。
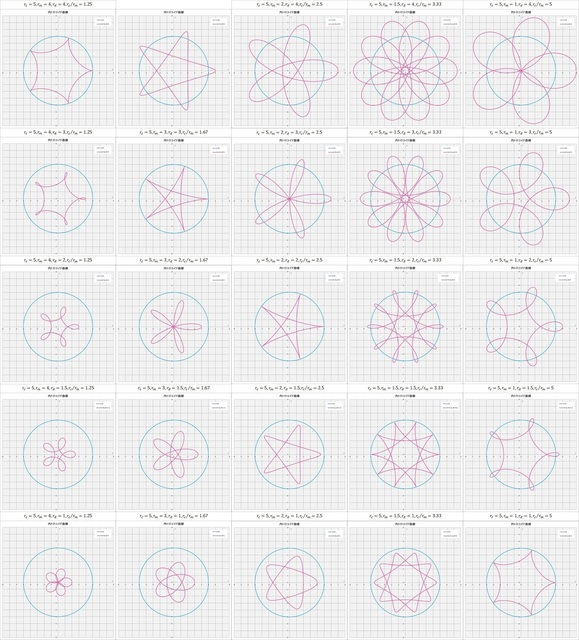
図3-10 \(r_c = 5,\,r_m = 4,\,3,\,2,\,1.5,\,1,\,r_d =4,\,3,\,2,\,1.5,1\) の場合の内トロコイド曲線
上の図を見ると、\(r_m\) と \(r_d\) の組み合わせで内トロコイド曲線の規則性が見てとれる。マトリックスの左上から右下にかけての対角の位置にある曲線は \(r_m = r_d\) なので曲線が定円に接するサイクロイド曲線になっている。それより左下の領域にある曲線は \(r_m > r_d\) なのでトロコイド曲線は定円に接することはなく、定円の内部で曲線が描かれることになる。一方、右上の領域にある曲線は \(r_m < r_d\) なのでトロコイド曲線は定円の外側にもはみ出した曲線となる。
定円と動円の半径の比 \(r_c / r_m\) の値に応じて花びらの数が変わるが、一番右側の列の \(r_c / r_m = 5/1\) の場合は動円は定円の周りを1周すれば描画点は元の位置に戻り、5個の花びらが描かれることになる。左側3列の \(r_c / r_m = 5/4,\,5/3,\,5/2\) の場合は、描画点が元の位置に戻るには動円は定円の周りをそれぞれ 4, 3, 2 周する必要があり、その時、そのいずれの場合も5個の花びらが描かれる。そして他の4列とは異なる形状の曲線が描かれる右から2番目の列の \(r_c / r_m = 5/1.5 = 10/3\) の場合は、動円が3周して初めて描画点が元の位置に戻り、10個の花びらが描かれる。
これからわかることは、外トロコイド曲線の場合と同じように、定円と動円の半径の比 \(r_c / r_m\) が、\(r_c,\,r_m\) がともに最小の整数の比 \(r'_c / r'_m\) で表される場合に、動円は定円の周りを \(r'_m\) 周してはじめて描画点が元の位置に戻り、\(r'_c\) 個の花びらが描かれるのだ。
外トロコイド曲線のところでも述べたが、もちろん、ここに示したのは内トロコイド曲線の一部で、\(r_c,\,r_m,\,r_d\) の組み合わせは無数に存在する。
つづく。
Date: 2022/07/2620220726
Title: 美しい曲線 トロコイド曲線の世界(その7)- 応用編1
Category: 数学
Keywords: 外トロコイド
これまでは、外トロコイドと内トロコイドの基本的な内容について書いてきたが、ここからはそれらの応用編について書いてみようと思う。(前回から随分時間が経ってしまったが…)
これまで見てきたように、トロコイド曲線は定円の周りを動円が1周または何周かすると描画点が最初の位置に戻ってくる。そして、定円の半径 \(r_c\) 、動円の半径 \(r_m\) 、描画点の半径 \(r_d\) の組み合わせは無数に存在する。そこで、よりきめ細やかな曲線を描くにはどうすればいいか、ということだが、それには定円と動円の半径の比 \(r_c / r_m\) が、\(r_c\) 、\(r_m\) がともに最小の整数の比 \(r'_c / r'_m\) で表される組み合わせのうち、\(r'_c\) が大きくなる組み合わせを選べばいいことになる。ただし、\(r'_m\) も大きくなるので、実際にスピログラフで曲線を描こうとすると、動円となる歯車を何周も何十周もグルグル回し続ける羽目になってしまうが…。
4.1 単独の外トロコイド曲線(その1)
それでは具体的に曲線を描いてみよう。まずは、単独の外トロコイド曲線の場合を考えてみる。
(1) \(r_m = 4.2,\,r_m = 4.0,\,r_d = 3.6\)
このケースでは、\(r_c / r_m = 4.2 / 4.0 = 21 / 20\) なので、動円が定円の周りを20周すると描画点は元の位置に戻り、21個の花びらが描かれることになる。また、\(r_m > r_d\) なので描画点は動円の内側にあって定円の内側には来ない。これは実際にスピログラフの2枚の歯車を使って書くことができる(ただし、ギア比が \(r_c / r_m = 21 / 20\) の歯車が必要だが)。図4-1 はこの場合の外トロコイド曲線を Excel を使って描いたものだ。中央の青い点線は定円を表している。
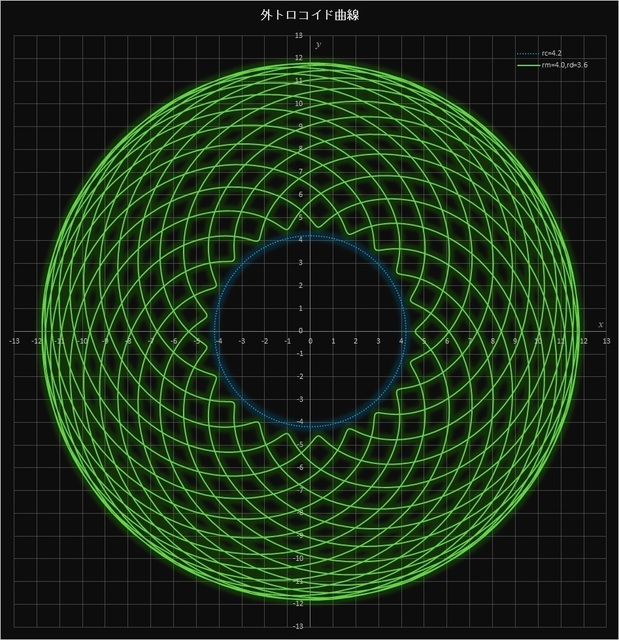
図4-1 \(r_c = 4.2,\, r_m = 4.0,\, r_d = 3.6\) の場合の外トロコイド曲線
図4-1 では曲線の色は単色だが、図4-2 では動円が1周するごとに色を変えて描いてみた(図では曲線に若干影をつけてある)。これは1周ごとに曲線を描き直さなければならないので、Excel のマクロ機能を使ってプログラミングしてもいいし、描画ソフトを使って描いてもいい。スピログラフでは1周ごとにペンの色を変えなければならないので、少々面倒だが…。

図4-2 \(r_c = 4.2,\, r_m = 4.0,\, r_d = 3.6\) の場合の外トロコイド曲線(動円が1周するごとに色を変えた場合)
(2) \(r_c = 3.85,\, r_m = 0.75,\, r_d = 0.5\)
このケースでは、\(r_c / r_m = 3.85 / 0.75 = 77 / 15\) なので、動円が定円の周りを15周すると描画点は元の位置に戻り、77個の花びらが描かれることになる。これも同様に \(r_m > r_d\) なので描画点は動円の内側にあって定円の内側には来ない。中央の青い点線は定円を表している。
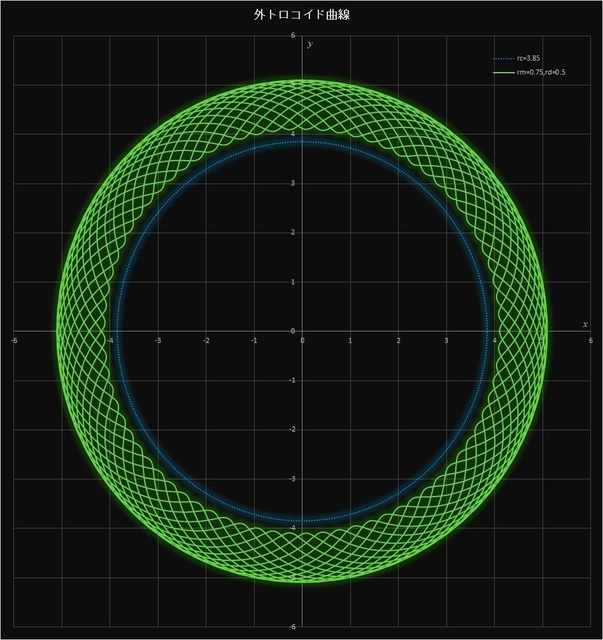
図4-3 \(r_c = 3.85,\, r_m = 0.75,\, r_d = 0.5\) の場合の外トロコイド曲線
図4-4 は同じように動円が1周するごとに色を変えて曲線を描いたものだ。
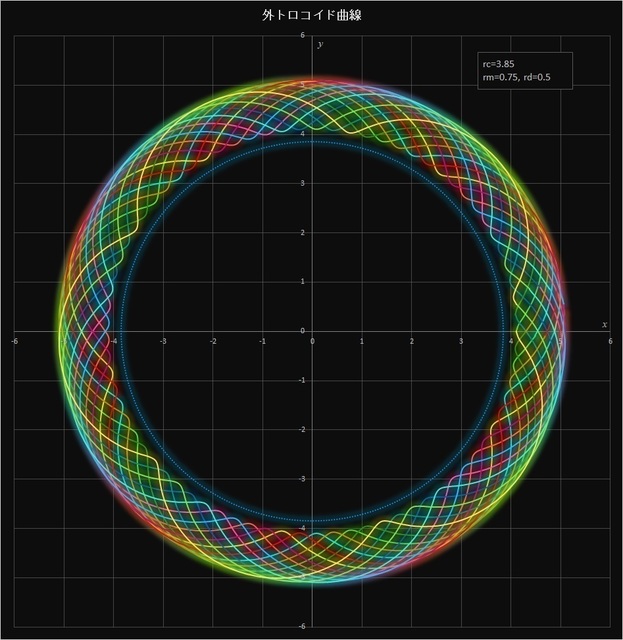
図4-4 \(r_c = 3.85,\, r_m = 0.75,\, r_d = 0.5\) の場合の外トロコイド曲線(動円が1周するごとに色を変えた場合)
(3) \(r_c = 4.3,\, r_m = 1.0,\, r_d = 3.6\)
このケースでは、\(r_c / r_m = 4.3 / 1.0 = 43 / 10\) なので、動円が定円の周りを10周すると描画点は元の位置に戻り、43個の花びらが描かれることになる。この場合は \(r_m < r_d\) なので描画点は動円の外側にあって定円の内側にまで入り込むので、PC上でExcelや描画ソフトなどを使って書くことはできるが、スピログラフでは描くことはできない。中央の青い点線(図では見にくいが)は定円を表している。
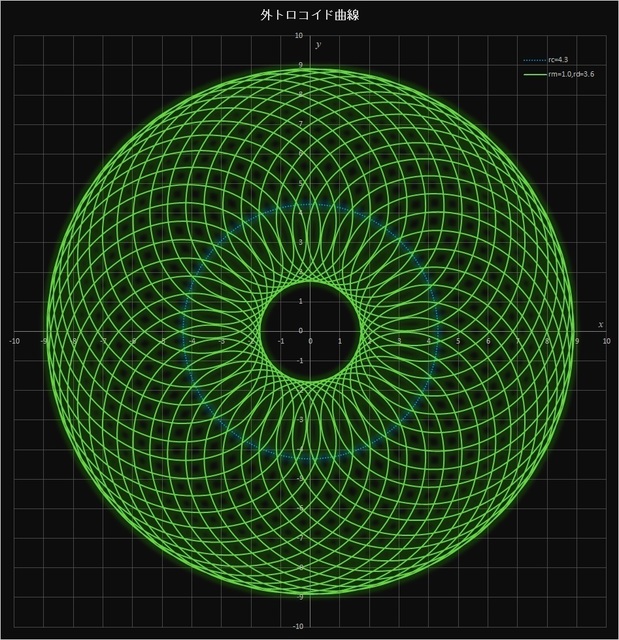
図4-5 \(r_c = 4.3,\, r_m = 1.0,\, r_d = 3.6\) の場合の外トロコイド曲線
つづく。
Date: 2022/07/2820220728
Title: 美しい曲線 トロコイド曲線の世界(その8)- 応用編2
Category: 数学
Keywords: 外トロコイド
前回はトロコイド曲線の応用編ということで、単独の外トロコイド曲線に具体的な例ついて書いてきたが、今回はさらに緻密な曲線を描かせたらどうなるか、いくつか例をあげてみよう。
4.2 単独の外トロコイド曲線(その2)- 緻密な曲線
(1) \(r_c = 10,\, r_m = 7.3,\, r_d = 8\)
このケースでは、\(r_c / r_m = 10 / 7.3 = 100 / 73\) となるが、この比の分母が素数となるような比を選んである(分子は分母の素数で割り切れなければ、素数である必要はない)。そして、動円が定円の周りを73周すると描画点は元の位置に戻ってくる。この場合は \(r_m < r_d\) で \(r_d\) がわずかに大きいので描画点は動円の外側にあって定円の内側にまで少しだけ入り込む。図4-6 の中央の青い点線(図では見にくいが)は定円を表している。
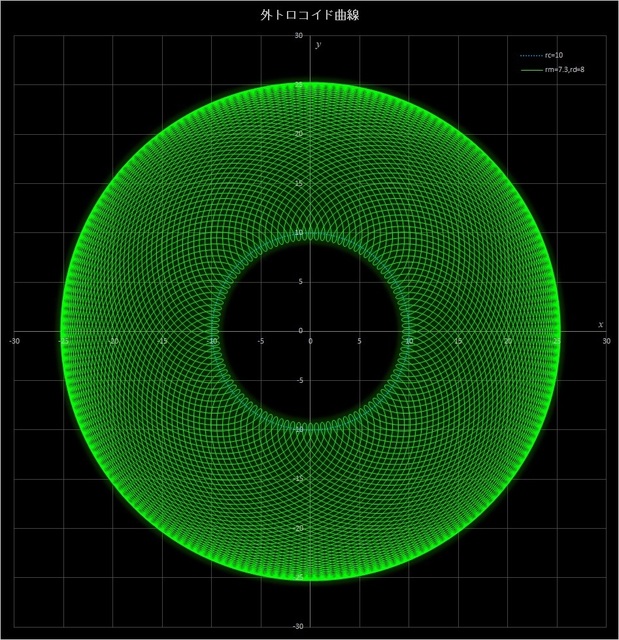
図4-6 \(r_c = 10,\, r_m = 7.3,\, r_d = 8\) の場合の外トロコイド曲線
(2) \(r_c = 10.1,\, r_m = 6.7,\, r_d = 12\)
このケースでは、\(r_c / r_m = 10.1 / 6.7 = 101 / 67\) となるが、この比の分母、分子共に素数となるような比を選んである。そして、動円が定円の周りを67周すると描画点は元の位置に戻ってくる。この場合は \(r_m < r_d\) なので描画点は動円の外側にあり、\(r_d\) が \(r_m\) の2倍近く大きいので定円のかなり内側にまで入り込む。そして、定円の内側でも曲線が交差するので特徴的なパターンが現れる。図4-7 の中央の青い点線(図では見にくいが)は定円を表している。
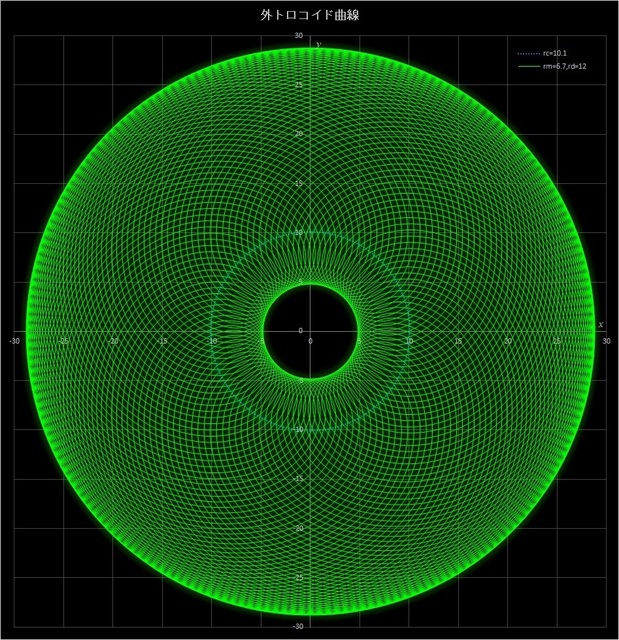
図4-7 \(r_c = 10.1,\, r_m = 6.7,\, r_d = 12\) の場合の外トロコイド曲線
(3) \(r_c = 3.79,\, r_m = 0.71,\, r_d = 0.5\)
このケースでは、\(r_c / r_m = 3.79 / 0.71 = 379 / 71\) となるが、この比の分母、分子共に素数となるような比を選んである。そして、動円が定円の周りを71周すると描画点は元の位置に戻ってくる。この場合は \(r_m > r_d\) なので描画点は動円の内側にあり、定円の内側まで入り込むことはない。図4-8 の中央の青い点線は定円を表している。
なお、曲線の中に縞模様が見えるが、これはかなり緻密な曲線を描いていることが影響している(描画ソフトで曲線を描き、倍率を変えると縞模様の位置が変わる)。

図4-8 \(r_c = 3.79,\, r_m = 0.71,\, r_d = 0.5\) の場合の外トロコイド曲線
(4) \(r_c = 2.3,\, r_m = 3.11,\, r_d = 4\)
このケースでは、\(r_c / r_m = 2.3 / 3.11 = 230 / 311\) となるが、分母が素数となるような比を選んである。そして、動円が定円の周りを311周すると描画点は元の位置に戻ってくる(311周もさせようとすると、計算も曲線を書かせるのも時間がかかって大変だが)。この場合は \(r_m < r_d\) なので描画点は動円の外側にあり、定円の内側まで入り込む。図4-9 では分かりずらいが中央付近に定円を青い点線で描いてある。さすがにここまでくると、全体が塗りつぶされたようになって、どのような曲線が描かれているのかはほとんどわからない。
なお、この図でも曲線の中に縞模様が見えるが、これはかなり緻密な曲線を描いていることが影響している(描画ソフトで曲線を描き、倍率を変えると縞模様の位置が変わる)。
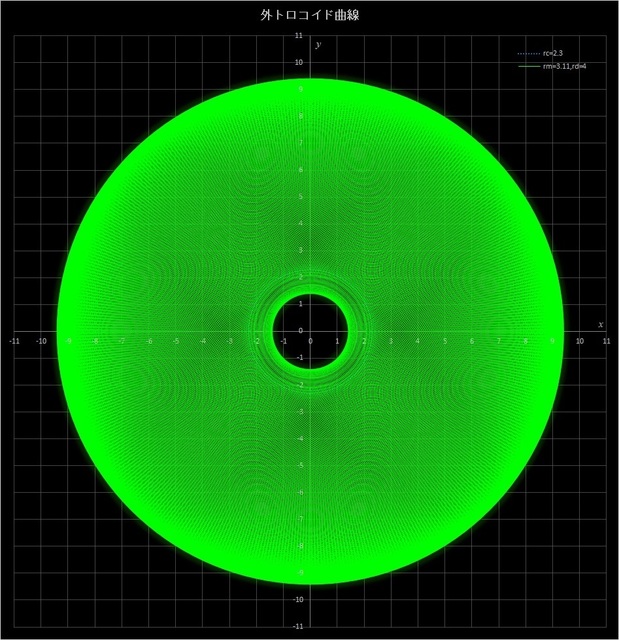
図4-9 \(r_c = 2.3,\, r_m = 3.11,\, r_d = 4\) の場合の外トロコイド曲線
ここまで見てきた例では、動円が定円の周りを回って描画点が元の位置に戻るまで曲線を描いてきたが、次回は途中で描くのを止めた場合、どのようなパターンが現れるか見ていこうと思う。
つづく。
Date: 2022/08/2820220828
Title: 美しい曲線 トロコイド曲線の世界(その9)- 応用編3
Category: 数学
Keywords: 外トロコイド
5.1 不完全な外トロコイド曲線
これまで見てきた例では、動円が定円の周りを回って描画点が元の位置に戻るまで曲線を描いてきたが(これを「完全トロコイド曲線」と呼ぶことにする)、何も最後まで曲線を描く必要はどこにもない(1周ずつ曲線を描いていけば途中でどのようなパターンになるかわかるが、一気に最後まで描いてしまうと途中で以下で示すようなパターンが現れることに気がつかないものだ)。
そこで、途中で曲線を描くのをやめた場合を「不完全トロコイド曲線」と呼ぶことにすると、どのようなパターンが現れるか以下の(1)〜(4)のケースで見ていってみよう。どこで止めるかによって現れるパターンは異なるので、いろいろ試して気に入ったパターンが現れたところで止めればよい(ただし、あまり早い段階で止めると、スカスカの曲線になってしまうが)。
(1) \(r_c = 10,\, r_m = 7.3,\, r_d = 8\) の場合の不完全外トロコイド曲線
このケースでは、動円が定円の周りを73周すると描画点が元の位置に戻って完全外トロコイド曲線が描かれるが、動円が65周したところで止めると、下の図のようなパターンが現れる。
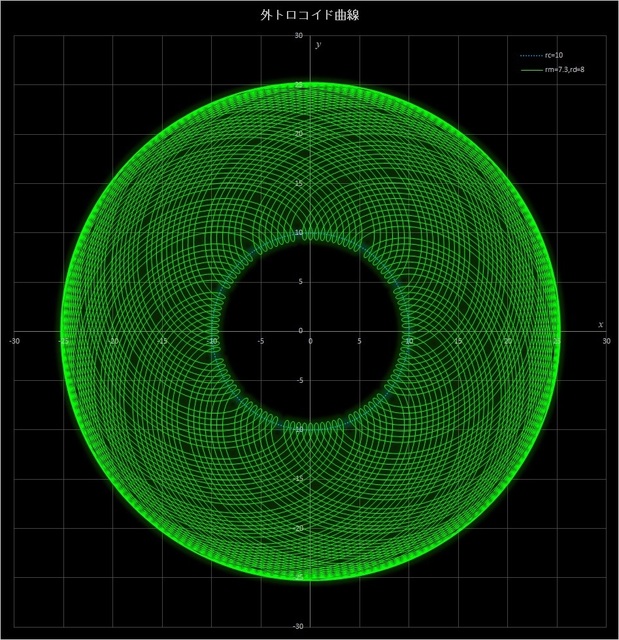
図5-1 \(r_c = 10,\, r_m = 7.3,\, r_d = 8\) の場合の外トロコイド曲線(動円が65周したところで止めた場合)
(2) \(r_c = 10.1,\, r_m = 6.7,\, r_d = 12\) の場合の不完全外トロコイド曲線
このケースでは動円が定円の周りを45.5周したところで止めてある。45.5周という中途半端なところで止めてあるのは、描画を止めた時、曲線の切れ目が目立たないようにするためだ。

図5-2 \(r_c = 10.1,\, r_m = 6.7,\, r_d = 12\) の場合の外トロコイド曲線(動円が45.5周したところで止めた場合)
(3) \(r_c = 3.79,\, r_m = 0.71,\, r_d = 0.5\) の場合の不完全外トロコイド曲線
このケースでは動円が定円の周りを45周したところで止めてある。

図5-3 \(r_c = 3.79,\, r_m = 0.71,\, r_d = 0.5\) の場合の外トロコイド曲線(動円が45周したところで止めた場合)
(4) \(r_c = 2.3,\, r_m = 3.11,\, r_d = 4\) の場合の不完全外トロコイド曲線
このケースでは動円が定円の周りを265周したところで止めてある。そうすることで、全体が塗りつぶされたような感じになっていたところに、あるパターンが現れてくる(それでも中心部分と外周はほとんど塗りつぶされたようになってしまっているが)。
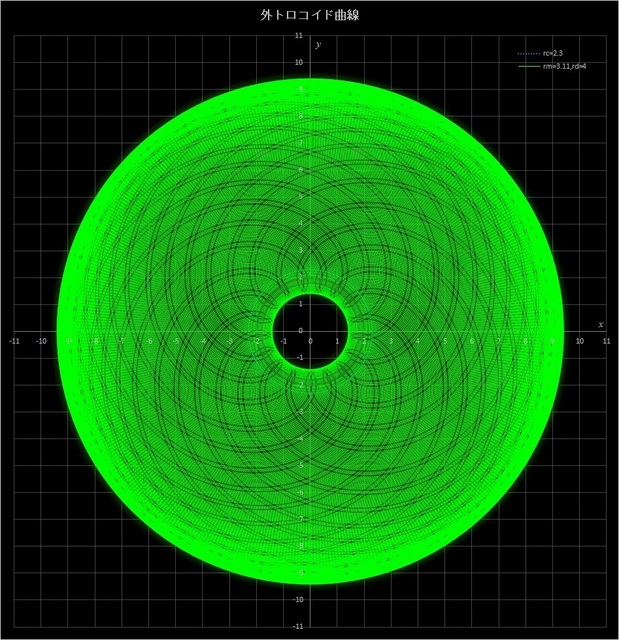
図5-4 \(r_c = 2.3,\, r_m = 3.11,\, r_d = 4\) の場合の外トロコイド曲線(動円が265周したところで止めた場合)
5.2 外トロコイド曲線の組み合わせ
これまでは単独の外トロコイド曲線を描いてきたが、ここでは複数の外トロコイド曲線を組み合わせて曲線を描いてみる。
(1) 2つの曲線(\(r_c = 5.3,\, r_m = 1.0,\, r_d = 3.4\) と \(r_c = 1.925,\, r_m = 0.375,\, r_d = 0.25\))の組み合わせ
このケースでは、応用編1の (2) および (3) で見てきた2つの曲線のパラメーター \(r_c,\, r_m,\, r_d\) を変えて組み合わせたものだ。大きな \(r_c = 5.3,\, r_m = 1.0,\, r_d = 3.4\) の曲線の中心に小さな \(r_c = 1.925,\, r_m = 0.375,\, r_d = 0.25\) の曲線が描かれている(図ではそれぞれの定円は省略してある)。

図5-5 2つの外トロコイド曲線(\(r_c = 5.3,\, r_m = 1.0,\, r_d = 3.4\,/\,r_c = 1.925,\, r_m = 0.375,\, r_d = 0.25\) を組み合わせた場合
これまでは外トロコイドの応用について書いてきたが、次回は内トロコイドの応用について書いてみたいと思う。
つづく。
Date: 2022/09/2920220929
Title: 美しい曲線 トロコイド曲線の世界(その10)- 応用編4
Category: 数学
Keywords: 内トロコイド
前回は外トロコイドの応用として不完全な外トロコイド曲線と外トロコイド曲線の組み合わせについて書いたが、ここからは内トロコイド曲線の応用について書いていこう。
6.1 単独の内トロコイド曲線(その1)
まずは単独の内トロコイド曲線をいくつか描いてみよう。
(1) \(r_c = 5.8,\, r_m = 4.5,\, r_d = 3.0\)
このケースでは、\(r_c\,/\,r_m = 5.8\,/\,4.5 = 58\,/\,45\) なので、動円が定円の周りを45周すると描画点は元の位置に戻り、58個の花びらが描かれることになる。また、\(r_m > r_d\) なので描画点は動円の内側にあって定円の外側には来ない。これは実際にスピログラフの2枚の歯車を使って書くことができる(ただし、ギア比が \(r_c\,/\,r_m = 58\,/\,45\) の歯車が必要で、描くのも大変だが)。図6-1 はこの場合の内トロコイド曲線を Excel を使って描いたものだ。緑の曲線の外側の青い点線は定円を表している。
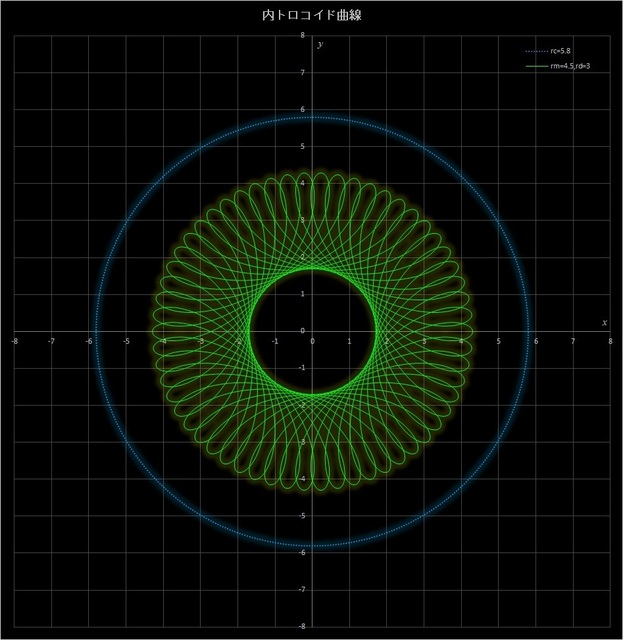
図6-1 \(r_c = 5.8,\, r_m = 4.5,\, r_d = 3.0\) の場合の内トロコイド曲線
(2) \(r_c = 5.8,\, r_m = 2.3,\, r_d = 3.5\)
このケースでは、\(r_c\,/\,r_m = 5.8\,/\,2.3 = 58\,/\,23\) なので、動円が定円の周りを23周すると描画点は元の位置に戻り、58個の花びらが描かれることになる。この場合は \(r_m < r_d\) なので描画点は動円の外側にあって定円の外側まではみ出してしまう。PC上で Excel や描画ソフトなどを使って書くことはできるが、スピログラフでは描くことはできない。青い点線は定円を表している。
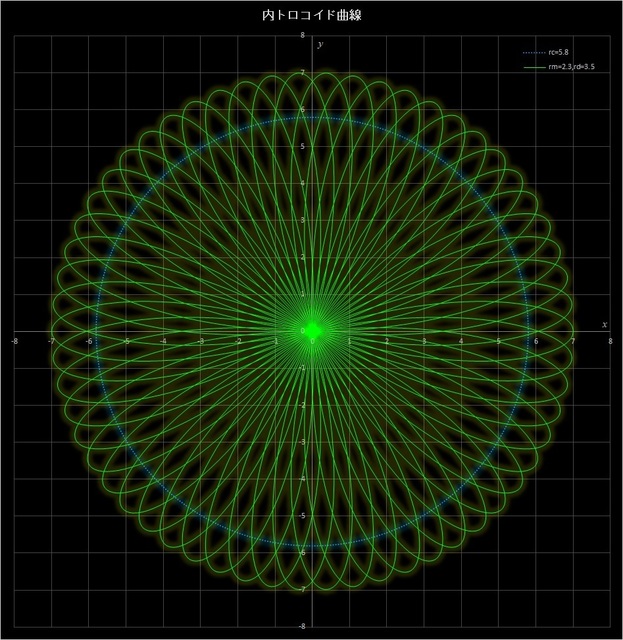
図6-2 \(r_c = 5.8,\, r_m = 2.3,\, r_d = 3.5\) の場合の内トロコイド曲線
(3) \(r_c = 6.25,\, r_m = 4.55,\, r_d = 10\)
このケースでは、\(r_c\,/\,r_m = 6.25\,/\,4.55 = 125\,/\,91\) なので、動円が定円の周りを91周すると描画点は元の位置に戻り、125個の花びらが描かれることになる。この場合は \(r_m < r_d\) なので描画点は動円の外側にあって定円の外側まではみ出してしまうが、描画点が最も外側に来た時、中心からの距離は \(|x| = |r_c - r_m + r_d| = |6.25 - 4.55 + 10| = 11.7\) となる。一方、描画点が最も内側に来た時の中心からの距離は\(|x| = |r_c - r_m - r_d| = |6.25 - 4.55 - 10| = 8.3\) となり、描画点は常に定円の外側にあり、下の図のように一見外トロコイド曲線のような曲線になる。この曲線はPC上で Excel や描画ソフトなどを使って書くことはできるが、スピログラフでは描くことはできない。青い点線は定円を表している。
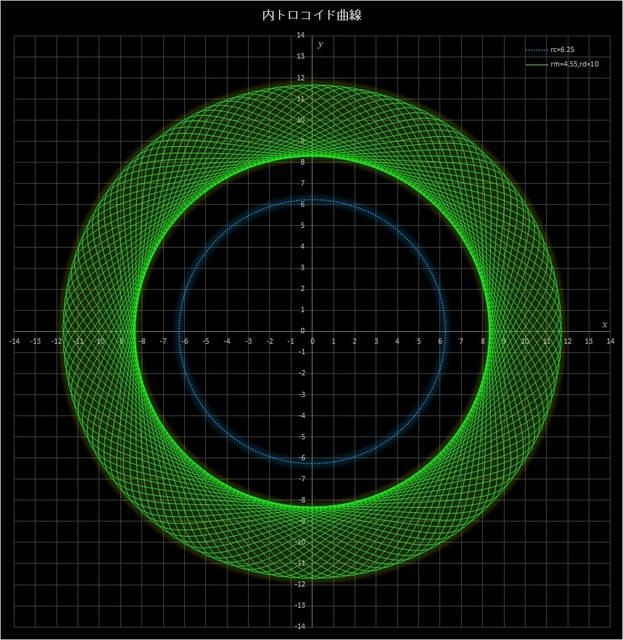
図6-3 \(r_c = 6.25,\, r_m = 4.55,\, r_d = 10\) の場合の内トロコイド曲線
6.2 単独の内トロコイド曲線(その2)- 緻密な曲線
次に、外トロコイド曲線の場合と同じように、これまでよりもっと緻密な曲線を描かせたらどうなるか、いくつか例をあげてみよう。
(1) \(r_c = 5,\, r_m = 2.51,\, r_d = 3\)
このケースでは、\(r_c\,/\,r_m = 5\,/\,2.51 = 500\,/\,251\) となるが、これまでの例と同様に、この比の分母が素数となるような比を選んである(分子は分母の素数で割り切れなければ、素数である必要はない)。そして、動円が定円の周りを251周すると描画点は元の位置に戻ってくる。この場合は \(r_m < r_d\) で \(r_d\) がわずかに大きいので描画点は動円の外側にあって定円の外側にまで少しだけはみ出す。曲線の外側から少し内側の青い点線(図では見にくいが)は定円を表している。
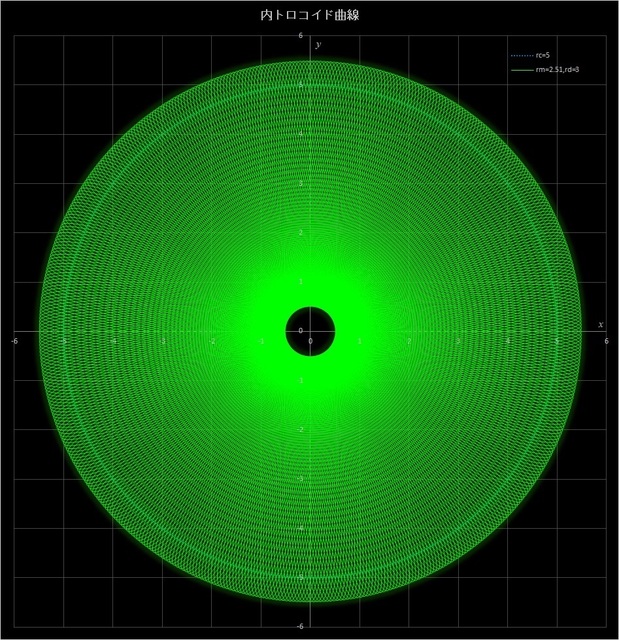
図6-4 \(r_c = 5,\, r_m = 2.51,\, r_d = 3\) の場合の内トロコイド曲線
図ではかなり細かい曲線が描かれているので、中央付近は塗りつぶされたようになって、太陽のコロナを彷彿させる状態になっている(中央のぽっかり空いた穴が遮蔽された太陽に見立てると)。
(2) \(r_c = 5,\, r_m = 3.13,\, r_d = 3\)
このケースでは、\(r_c\,/\,r_m = 5\,/\,3.13 = 500\,/\,313\) となるが、これも、この比の分母が素数となるような比を選んである。そして、今度は動円が定円の周りを313周してやっと描画点が元の位置に戻ってくる。この場合は \(r_m > r_d\) で \(r_m\) がわずかに大きいので描画点は動円の内側にあって定円の外側にははみ出さない。曲線の少し外側の青い点線は定円を表している。
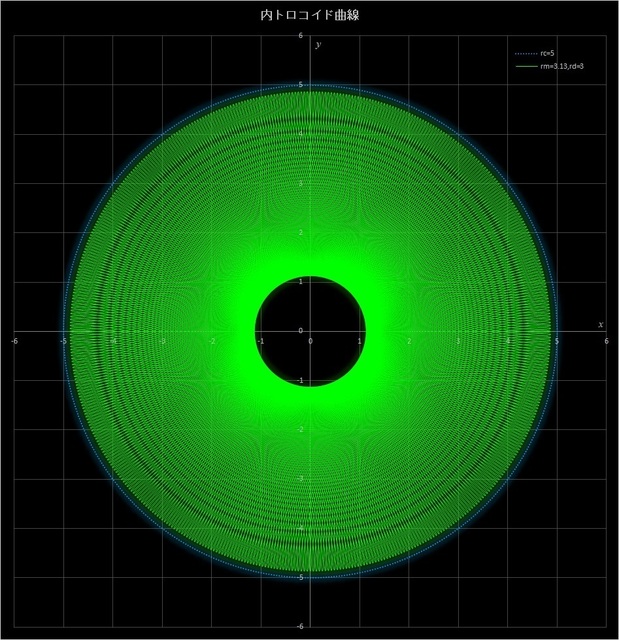
図6-5 \(r_c = 5,\, r_m = 3.13,\, r_d = 3\) の場合の内トロコイド曲線
この図でもかなり細かい曲線が描かれているので、前の例と同じように中央付近は塗りつぶされたようになって、太陽のコロナのような状態になっているが、外側に行くにつれて同心円状のパターンが現れる。パターンが現れるポイントは曲線が交差している位置だ。
なお、同心円状のパターンと中心部の間にも縞模様が見えるが、これはかなり緻密な曲線を描いていることが影響している(描画ソフトで曲線を描き、倍率を変えると縞模様の位置が変わったり、消えたりする)。
つづく。
Date: 2022/10/2920221029
Title: 美しい曲線 トロコイド曲線の世界(その11)- 応用編5
Category: 数学
Keywords: 内トロコイド
前回は単独の内トロコイド曲線について書いたが、ここからは不完全な内トロコイド曲線について書いていこう。
7.1 不完全な内トロコイド曲線
これまで見てきた例では、動円が定円の周りを回って描画点が元の位置に戻るまで曲線を描いてきたが「完全内トロコイド曲線」だ。そこで、その9-応用編3の場合と同じように、途中で曲線を描くのをやめた「不完全内トロコイド曲線」について見ていってみよう。どこで止めるかによって現れるパターンは異なるので、いろいろ試して気に入ったパターンが現れたところで止めればよい。
(1) \(r_c = 5,\, r_m = 2.51,\, r_d = 3\) の場合の不完全内トロコイド曲線
このケースでは、動円が定円の周りを 251 周すると描画点が元の位置に戻って完全内トロコイド曲線が描かれるが(その10-応用編4の図6-4)、その 1/4 の 62.75 周、1/2 の 125.5 周、3/4 の 188.25 周したところで止めると、下の3つの図のようなパターンが現れる。
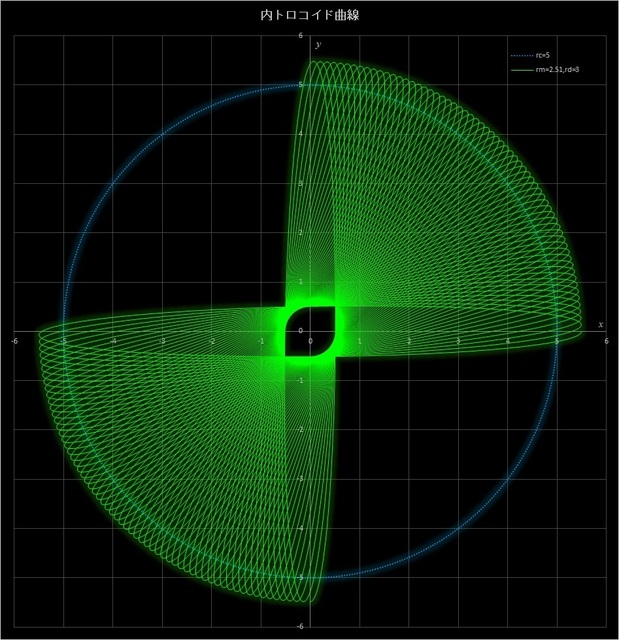
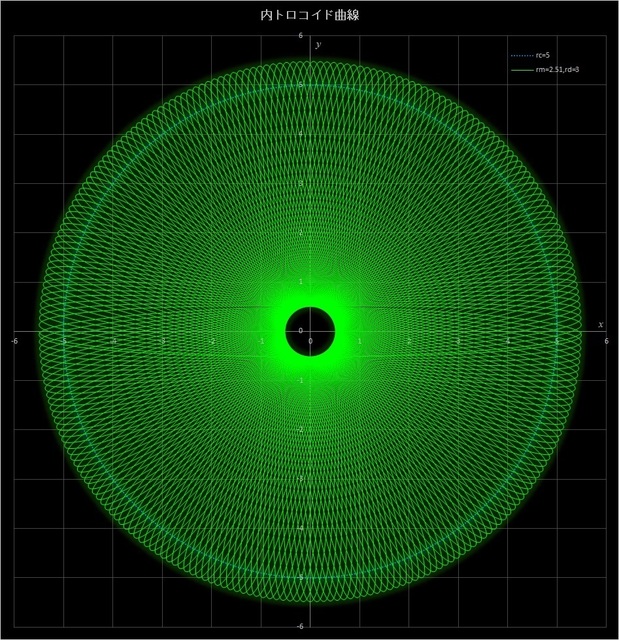
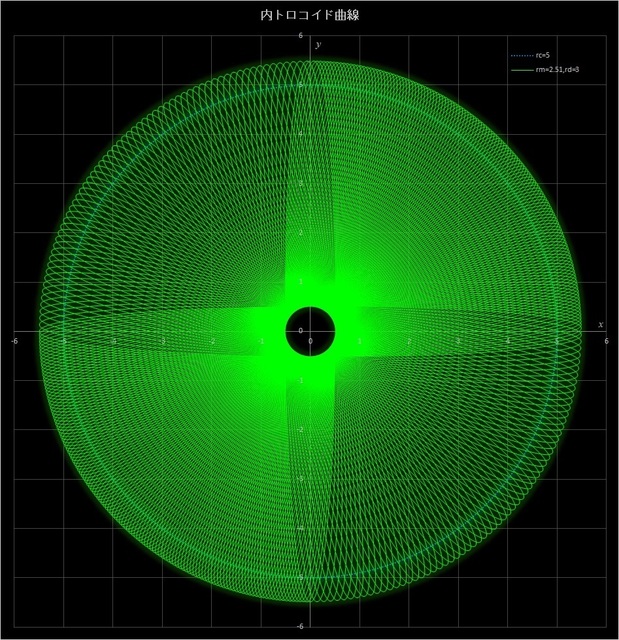
図7-1 \(r_c = 5,\, r_m = 2.51,\, r_d = 3\) の場合の内トロコイド曲線(動円が62.75周(上)、125.5周(中)、
188.25周(下)したところで止めた場合)。最後にはその10-応用編4の図6-4のようになる。
(2) \(r_c = 5,\, r_m = 3.13,\, r_d = 3\) の場合の不完全内トロコイド曲線
このケースでは、動円が定円の周りを 313 周すると描画点が元の位置に戻って完全内トロコイド曲線が描かれるが(その10-応用編4の図6-5)、30.5 周、100 周、216 周、275 周したところで止めると、下の4つの図のようなパターンが現れる。動円の周回数が増えるにつれて、星型のパターンが変わっていくのがわかる。
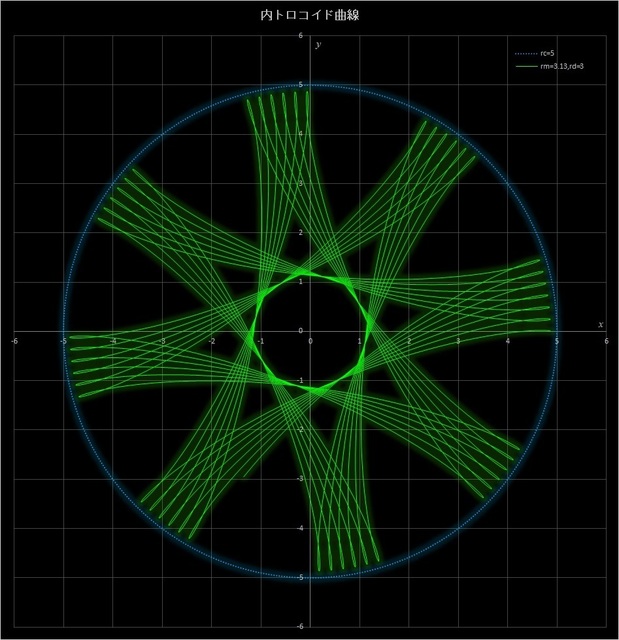
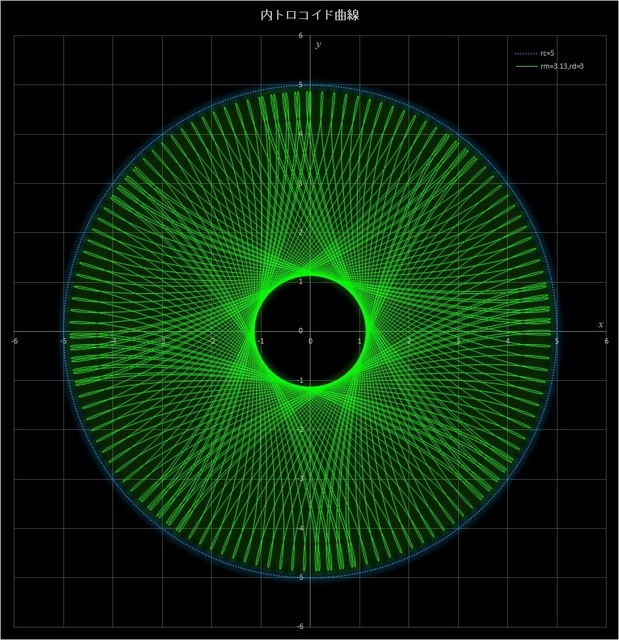
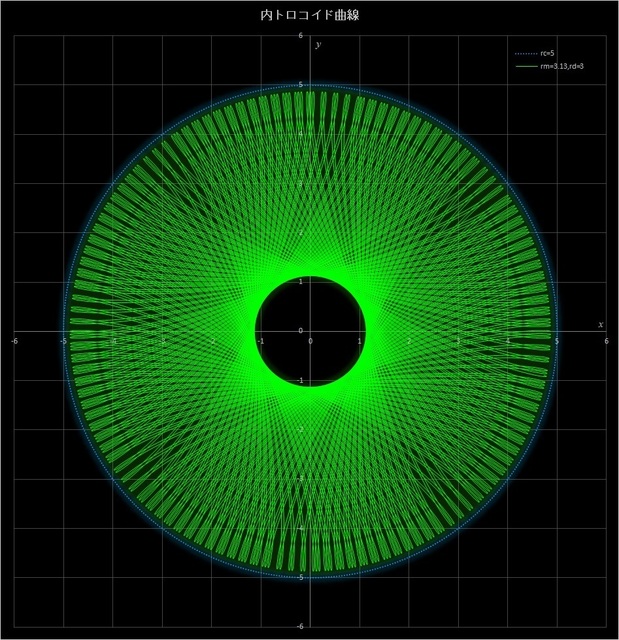
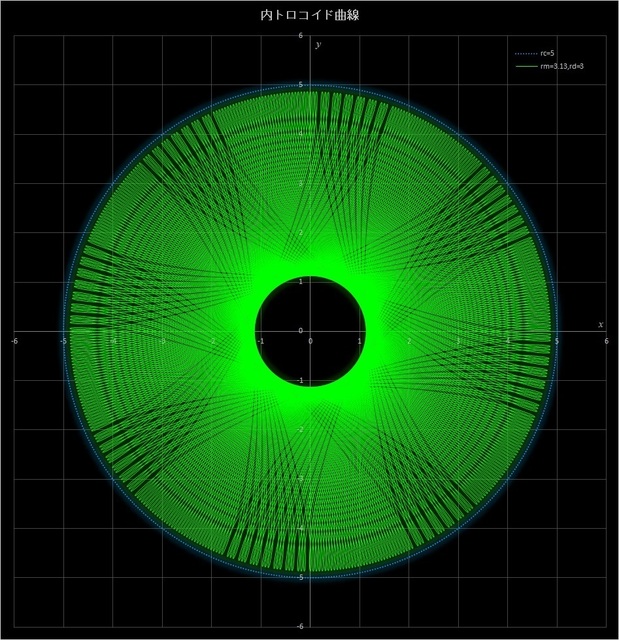
図7-2 \(r_c = 5,\, r_m = 3.13,\, r_d = 3\) の場合の内トロコイド曲線(動円が 30.5 周(一番上)、100 周(2番目)、
216 周(3番目)、275 周(一番下)したところで止めた場合)。最後にはその10-応用編4の図6-5のようになる。
(3) リボン型の不完全内トロコイド曲線
ここでは、曲線の形がリボン型になる不完全内トロコイド曲線の例を2つ紹介しよう。
①まずは、\(r_c = 7.3,\, r_m = 3.13\) で \(r_d = 1,\,2,\,3,\,4\) と変えてみた場合の不完全内トロコイド曲線だ(青点線の円は定円を表している)。この例では動円が定円の周りを313周すると描画点が元の位置に戻ってくるが、4つとも45周したところで止めてある。このケースでは \(r_d\) が多きくなるにつれて曲線がシャープになっていき、中央部の星型のパターンが小さくなっていくのがわかる。
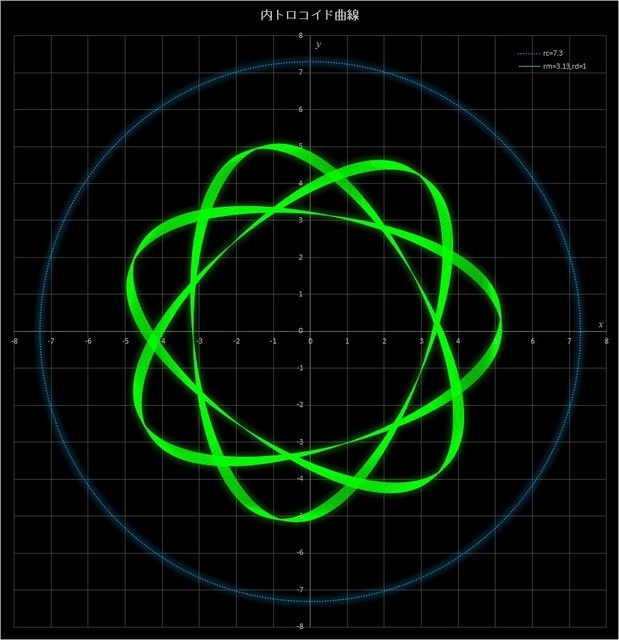
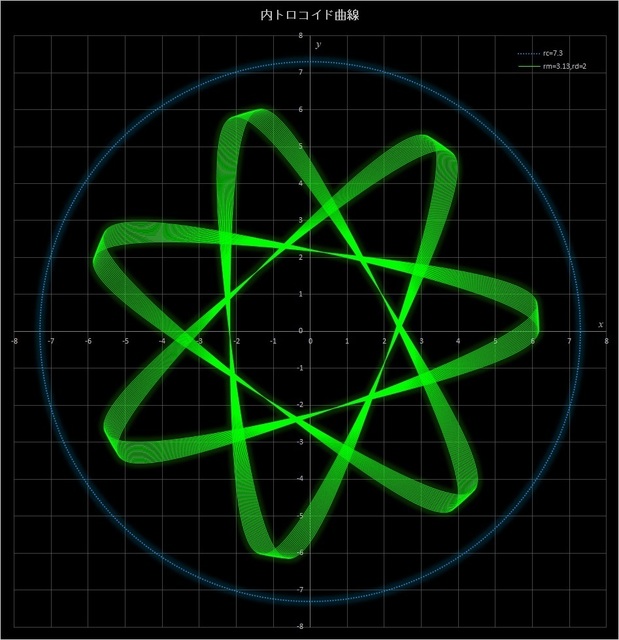
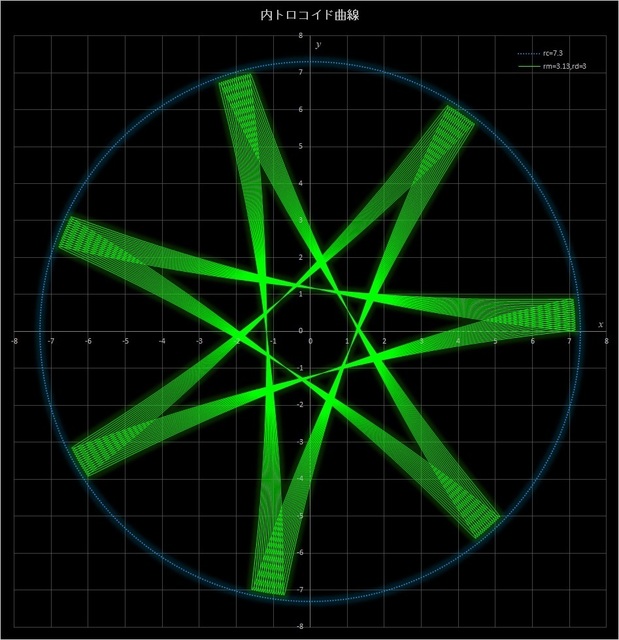
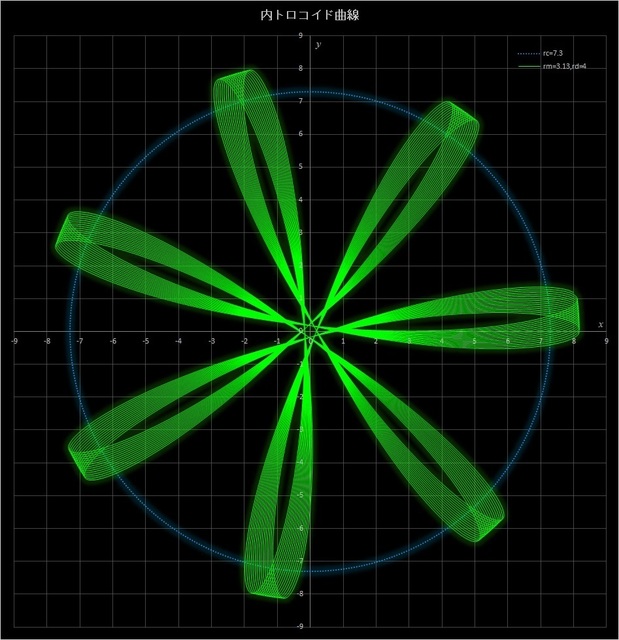
図7-3 \(r_c = 7.3,\, r_m = 3.13\) に固定して \(r_d = 1,\,2,\,3,\,4\) と変えた場合の不完全内トロコイド曲線
(動円は45周したところで止めてある)。一番上:\(r_d = 1\)、2番目:\(r_d = 2\)、3番目:\(r_d = 3\)、一番下:\(r_d = 4\)
②次のケースでは、\(r_c = 9,\, r_m = 3.13\) で \(r_d = 4,\,5,\,6,\,7\) と変えてみた場合の不完全内トロコイド曲線だ(青点線の円は定円を表している)。この例では動円が定円の周りを 313 周すると描画点が元の位置に戻ってくるが、3つとも 120 周したところで止めてある。このケースでは \(r_d\) が多きくなるにつれて外周部のリボンの折れ曲り具合が緩やかになり、中央部の円形の隙間がが小さくなっていき、その後再び大きくなっているのがわかる(\(r_d = r_c - r_m = 5.87\) のとき、中央の隙間はなくなる)。それに伴って中心部分の曲線が交差することでできるパターンが変化していく。
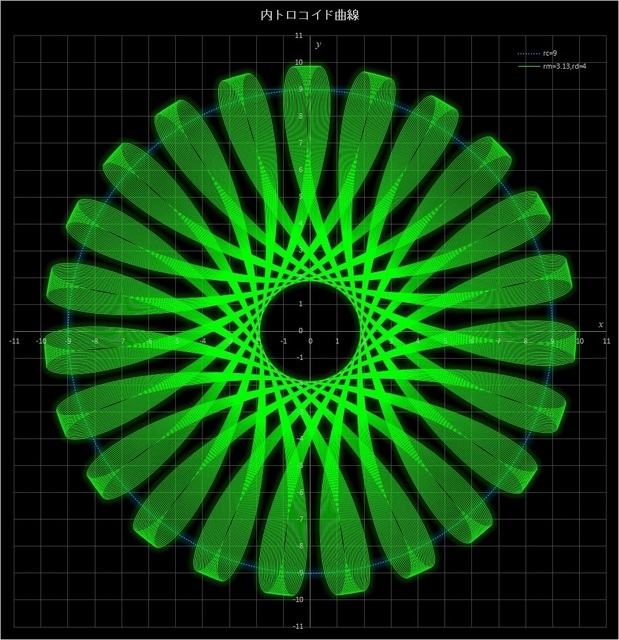
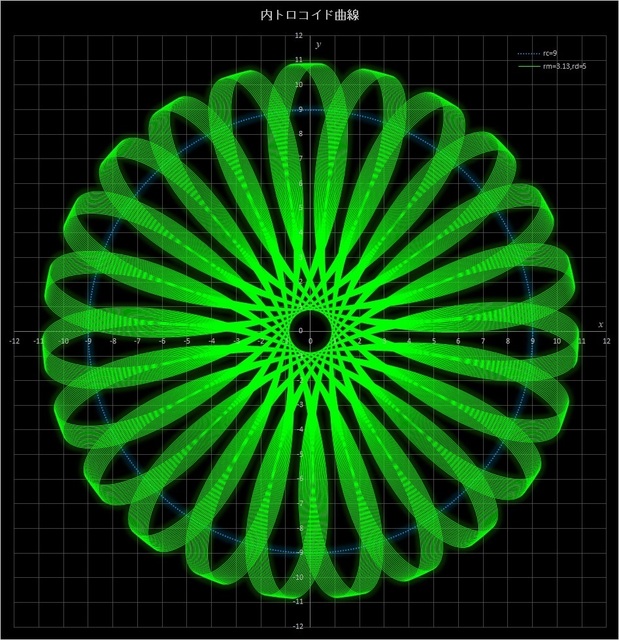
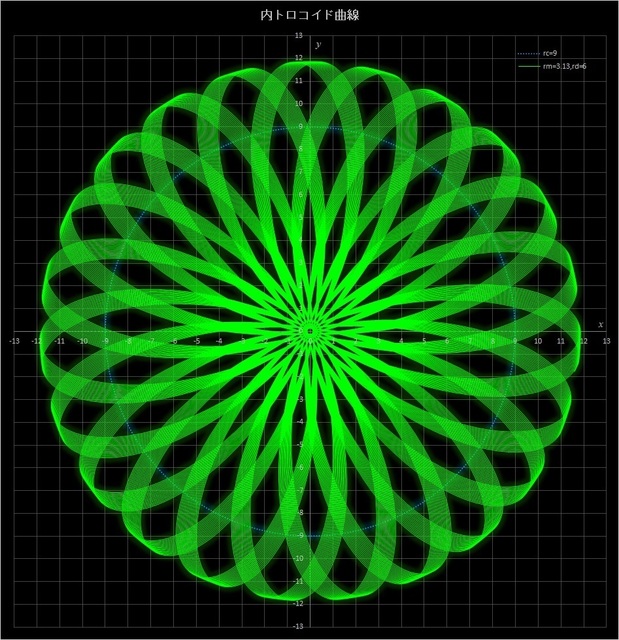

図7-4 \(r_c = 9,\, r_m = 3.13\) に固定して \(r_d = 4,\,5,\,6,\,7\) と変えた場合の不完全内トロコイド曲線
(動円は120周したところで止めてある)。一番上:\(r_d = 4\)、2番目:\(r_d = 5\)、3番目:\(r_d = 6\)、一番下:\(r_d = 7\)
つづく。
Date: 2022/11/2020221120
Title: 美しい曲線 トロコイド曲線の世界(その12)- 応用編6
Category: 数学
Keywords: 内トロコイド
前回は単独かつ不完全な内トロコイド曲線について書いたが、ここでは複数の内トロコイド曲線を組み合わせて曲線を描いてみよう。
8.1 内トロコイド曲線の組み合わせ
(1) 2つの曲線(\(r_c = 6.25,\, r_m = 4.55,\, r_d = 10\) と \(r_c = 6.3,\, r_m = 2.3,\, r_d = 4\))の組み合わせ
このケースでは、応用編4-単独の内トロコイド曲線(その1)の (2) および (3) で見てきた2つの曲線のパラメーター \(r_c,\, r_m,\, r_d\) を変えて組み合わせたものだ。円環状の \(r_c = 6.25,\, r_m = 4.55,\, r_d = 10\) の曲線の中に小さな \(r_c = 6.3,\, r_m = 2.3,\, r_d = 4\) の曲線が描かれている(図ではそれぞれの定円は省略してある)。
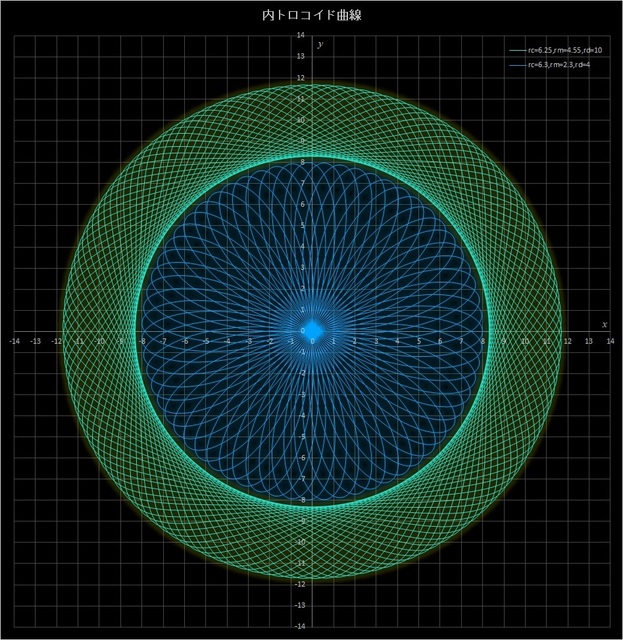
図8-1 2つの内トロコイド曲線(\(r_c = 6.25,\, r_m = 4.55,\, r_d = 10\,/\,r_c = 6.3,\, r_m = 2.3,\, r_d = 4\))を組み合わせた場合
(2) 2つの曲線(\(r_c = 6.26,\, r_m = 4.55,\, r_d = 10\) と \(r_c = 5.9,\, r_m = 2.14,\, r_d = 4\))の組み合わせ
このケースも応用編4-単独の内トロコイド曲線(その1)の (2) および (3) で見てきた2つの曲線のパラメーター \(r_c,\, r_m,\, r_d) を変えて組み合わせたものだ。円環状の \(r_c = 6.26,\, r_m = 4.55,\, r_d = 10\)の曲線の中に小さな \(r_c = 5.9,\, r_m = 2.14,\, r_d = 4\) の曲線が描かれている(図ではそれぞれの定円は省略してある)。ただし、このケースではどちらの曲線も描画点が元の位置に戻るまでは描かれておらず、外側の曲線は動円が定円の周りを90周、内側の曲線は88周させたところで描画点を止めてある。こうすることで図のようなパターンが見えてくる。(描画点が元の位置に戻ってくるまでには、外側の曲線では動円は定円の周りを455周、内側の曲線では107周させる必要がある)。
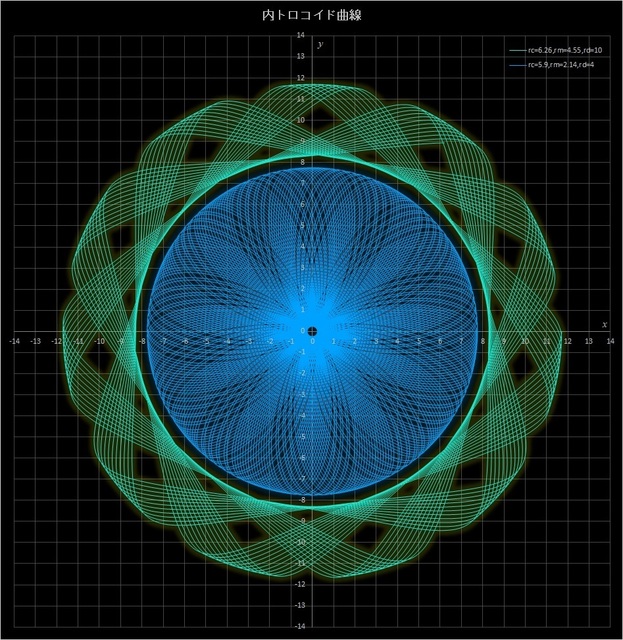
図8-2 2つの内トロコイド曲線(\(r_c = 6.26,\, r_m = 4.55,\, r_d = 10\,/\,r_c = 5.9,\, r_m = 2.14,\, r_d = 4\))を組み合わせた場合
ここで紹介した曲線はほんの一例で、\(r_c,\, r_m,\, r_d\) の組み合わせは無数に存在するので、皆さんもパラメータを変えて描いてみて、気に入った曲線を探してみてください。
このシリーズはこれで一応終わりとします。

|

|