かがくのつまみ食い
― 一様な重力の中の運動 ―

Date: 2024/01/13
Title: 一様な重力の中の運動：巨大真空室中での自由落下 － ガリレオは正しかった
Category: 物理
Keywords: 一様な重力、自由落下、ガリレオ

1. 真空中での自由落下

X（旧Twitter）で興味深い動画を見た。

それは、英国の物理学者ブライアン・コックス（Brian Cox）が、英BBCのドキュメンタリー番組『Human Universe』の一編で、NASAの世界最大の真空室を訪れたときに行われた実験の様子を収めたものだ。その実験とは、真空中の一様な重力場で、二つの物体（ボウリングのボールと羽）を同時に落下させて、その様子を記録したものだ。

以下は同番組のYouTube映像


僕らが経験的に知っているのは、空気中であれば、羽の方が空気抵抗が大きいので、羽よりボールの方が早く床に落ちる。しかし、真空中であれば、空気抵抗がないので、ボールと羽は同時に床に落ちる。

もう少し具体的に書くと
一様な重力場、例えば地表近くでの重力は、空間的には近似的に一様と見なすことができるので、そのような空間での落下運動を考える。
質量 \(m\) の物体に働く重力は、重力加速度を \(g\) とすると、\(F = mg\) だ。本来は重力および重力加速度はベクトル量だが、鉛直方向の成分しか持たないので、鉛直上向きの方向を \(z\) 軸として、\(z\) 軸方向の運動のみを考える。

重力以外の外力を受けない場合の運動、すなわち自由落下の場合、運動方程式は以下の通りだ。
\begin{align} & m\frac{d^2z}{dt^2}=-mg \\ & \\ & \therefore \, \frac{d^2z}{dt^2}=-g \quad\quad\quad (1) \end{align} これは、物体の質量にはよらないことを意味している。したがって、空気抵抗など重力以外の外力がない場合は、ボウリングのボールと羽は同時に落ちることになる。

さて、これを解くには、式 (1) を積分してやればよいが、初期条件を与えなければならない。そこで、\(t = 0\) のときの速度と位置をそれぞれ \(v_{z0}\) 、\(z_0\) とすると、
\begin{align} v_z=\frac{dz}{dt}=-\int{g}dt=-gt+C_1 \end{align} ここで、\(t = 0\) のとき \(v_z=v_{z0}\) なので、\(C_1 = v_{z0}\)
したがって、
\begin{align} v_z=-gt+v_{z0} \quad\quad\quad (2) \end{align} となる。さらに積分してやれば、
\begin{align} z=\int{(-gt+v_{z0})}dt=-\frac{1}{2}gt^2+v_{z0}t+C_2 \end{align} ここで、\(t = 0\) のとき \(z = z_0\) なので、\(C_2 = z_0\)
したがって、
\begin{align} z=-\frac{1}{2}gt^2+v_{z0}t+z_0 \quad\quad\quad (3) \end{align} となる。

さらに、具体的に地面（\(z = 0\)）から高さ \(z_0 = 1.6\,\rm m\) の高さから物体をゆっくり落とした場合（\(v_{z0} = 0\)）、物体が地面に着地するまでの時間とそのときの速度は式(2),(3)から（重力加速度は \(g = 9.8\,\rm m/s^2\)）
\begin{align} & -\frac{1}{2}gt^2+z_0=0 \quad\quad\quad (4) \\ & \therefore \,t=\sqrt{2z_0/g}=\sqrt{2\times 1.6/9.8 }=0.57\,\rm s \quad\quad\quad (5) \\ & v_z=-gt=-9.8\times0.57=-5.6\, \rm m/s\, (鉛直下向きに 5.6 m/s) \quad\quad\quad (6) \\ \end{align} となる。実際に \(1.6\,\rm m\) の高さから消しゴム（重さ数グラムかな？空気抵抗は無視できるとして）を落としてそれまでの時間を繰り返し5回測ったら、平均で \(t = 0.568\,\rm s\) だった。
お〜、合っているね！（さすがに速度までは測れなかったけど）
消しゴムのようなの小さな物は、\(1.6\,\rm m\) 程度の高さから落としたくらいでは、空気抵抗の効果は無視できるほど小さいのだ。これがもっと高いところから落とすと無視できなくなるけど。

さて、最初の話に戻ると、物理学者ブライアン・コックスがNASAの世界最大の真空室を訪れて、ボウリングのボールと羽を落として、その落下の様子を記録したものだが、最初、空気中で行った時は、当然ながら羽はゆっくりと落ちてくるので、ボールと羽は同時には落ちないが、その後、部屋の中を真空にして実験すると、ものの見事にボールと羽は同時に落ちていく様子が、スローモーション映像ではっきりと映し出されている。

今から53年前の1971年のアポロ15号の月面着陸ミッションでは、船長のデヴィッド・スコットが月面でハンマー（重さ\(1.32\,\rm kg\)）と鷹の羽（重さ \(0.03\,\rm kg\)）を約 \(1.6\,\rm m\) の高さから同時に落とし、同時に着地することを実演して見せたが、今ではわざわざ月まで行かなくても、地球上の巨大な真空室の中で同じ実験ができるようになったのだ。

自由落下する時間は式(5)から明らかなように物体の質量には依らず、落下する距離は落下時間の2乗に比例するのだ（式(4)）。これは「落体の法則」と呼ばれるもので、ガリレオが発見した法則なのだ。これに関して、ガリレオはピサの斜塔の上から砲弾の玉と木のボールを同時に落とし、両者が同時に着地する実験をしたという逸話が残っているが、実際にガリレオはこの実験をやったかどうかはわからないが、ガリレオの主張は正しかったのだ。

関連記事、Webサイトはこちら
X（旧Twitter）にアップされた映像：
https://twitter.com/gunsnrosesgirl3/status/1511795922694737923
Science Time の記事：
https://www.sciencetime.jp/note/234
BBCのドキュメンタリー番組『Human Universe』の一編：
https://www.bbc.co.uk/programmes/p02985m0
NASAのアポロ15号の月面での実験：
https://nssdc.gsfc.nasa.gov/planetary/lunar/apollo_15_feather_drop.html
月面実験の映像：
https://nssdc.gsfc.nasa.gov/planetary/image/AS15_Ham_feath_drop.mp4

Date: 2024/02/2320240223
Title: 一様な重力の中の運動：空気抵抗がある場合の落下運動(1)
Category: 物理
Keywords: 一様な重力、自由落下、空気抵抗

2. 速度に比例する空気抵抗があるの場合の自由落下①

前回は重力以外の外力がない場合の自由落下について書いたが、今回は空気抵抗がある場合の落下運動について書いてみようと思う。

空気抵抗は物体の速度があまり大きくない場合は速度に比例するので、空気抵抗は \(kv\) と表される。ここで、\(v\) は物体の速度、\(k\) は比例定数。この場合の質量 \(m\) の物体の運動方程式は鉛直下向きに \(z\) 軸をとると、
\begin{align} & m\frac{d^2z}{dt^2}=mg-kv \,（g：重力加速度）\\ & \\ & v=\frac{dz}{dt}\,なので、m\frac{dv}{dt}=mg-kv \\ & \\ & \therefore\,\frac{dv}{dt}=-\frac{k}{m}\big(v-\frac{mg}{k}\big) \quad\quad\quad\quad(1) \end{align} この式を解くには、変数分離して積分してやればいいわけだ。
\begin{align} & \frac{dv}{v-\frac{mg}{k}}=-\frac{k}{m}dt\,\,\rightarrow\,\,\int{\frac{dv}{v-\frac{mg}{k}}}=-\frac{k}{m}\int{dt} \\ & \\ & \ln{\big(v-\frac{mg}{k}\big)}=-\frac{k}{m}t+C \,（C：積分定数） \\ & \\ & \therefore\,v-\frac{mg}{k}=A\exp{\big(-\frac{k}{m}t\big)}\quad ただし、A=e^C \end{align} ここで、初期条件を \(t = 0\) のとき \(v = 0\) とすると \(A = -mg/k\) となるので、
\begin{align} v=\frac{mg}{k}\big[1-\exp{\big(-\frac{k}{m}t\big)}\big] \quad\quad\quad\quad(2) \end{align} 式(2)から、\(t \rightarrow \infty \) のときの速度は
\begin{align} v_t=\frac{mg}{k} \quad\quad\quad\quad(3) \end{align} これが終端速度（terminal velocity）と呼ばれるものだ。
次に、式(2)を積分してやると、
\begin{align} z & =\frac{mg}{k}\int{\big[1-\exp{\big(-\frac{k}{m}}\big)\big]}dt \\ & =\frac{mg}{k}t+\frac{m^2g}{k^2}\exp{\big(-\frac{k}{m}t\big)}+D \end{align} ここで、初期条件として \(t = 0\) のとき \(z = 0\) とすると、\(D = -m^2g/k^2\) となので、
\begin{align} \therefore\,z=\frac{mg}{k}t+\frac{m^2g}{k^2}\big[\exp{\big(-\frac{k}{m}t\big)}-1\big] \quad\quad\quad\quad(4) \end{align} となる。式(4)から \(t \rightarrow \infty\) の極限をとってやると \(\exp{(-kt/m)} \rightarrow 0\) なので、
\begin{align} z\simeq\frac{mg}{k}t-\frac{m^2g}{k^2} \end{align} と近似できるので、この式からも十分時間が経った後では物体は終端速度 \(v_f = mg/k\) で等速直線運動をするがわかる。

Date: 2024/03/0920240309
Title: 一様な重力の中の運動：空気抵抗がある場合の落下運動(2)
Category: 物理
Keywords: 一様な重力、自由落下、空気抵抗

3. 速度に比例する空気抵抗があるの場合の自由落下②

前の記事では、速度に比例する空気抵抗を受ける場合の落下運動の概略について書いてきた。ここからは具体的に見ていってみよう。

まずは、空気抵抗がない場合で、\(\rm 2000\,m\) の高さから落下してくる雨粒の落下速度を考えてみる。
この場合、\(y=(1/2)gt^2\) から、地上に到達するまでの時間は
\begin{align} t=\sqrt{2y/g}=\sqrt{2\times2000/9.8} \simeq 20.3\,\rm s \end{align} なので、地上に到達するときの速度は
\begin{align} v=gt=9.8\times 20.2 \simeq 200\, \rm m/s\,(720\, km/h) \end{align} と、とっても大きな値となる（ジェット旅客機の巡航速度は大体 \(900\,\rm km/h\) なので、それより少し遅い値だ）。こんな速度で雨粒が降ってきたら、頑丈な建物の中に避難しないと、命が危険にさらされる。

これを踏まえて、空気抵抗がある場合の落下運動を考えてみよう。
ここで考えているのは、落下する物体に働く空気抵抗が速度に比例する場合で、この場合の抵抗は粘性抵抗と呼ばれる。そこで、雨粒の落下を考えると、雨粒を半径 \(a\) の球（剛体球と仮定）とし、空気の粘度を \(\eta\) とすると、このときの空気抵抗 \(kv\) の比例定数 \(k\) はストークスの法則から
\begin{align} k=6\pi\eta a \end{align} で表される（天下り式に書いたが）。
水の密度を \(\rho\) とすると、雨滴の質量は \((4/3)\pi a^3 \rho\) より、終端速度は
\begin{align} v_t=\frac{mg}{k}=\frac{\frac{4}{3}\pi a^3 \rho g}{6\pi\eta a}=\frac{2a^2\rho g}{9\eta} \end{align} となる。

そこで、具体的に数値を当てはめてみると、雨粒の半径を \(a = 1 \times 10^{-3}\,\rm m\,(1 mm)\) として、水の密度 \(\rho = 1.0 \times 10^3\,\rm kg/m^3\) 、空気の粘度 \(\eta = 1.8 \times 10^{-5}\,\rm Pa \cdot s\)（\(\rm 0^{\circ}C\)、1気圧\(= 0.1\,\rm MPa\)）、重力加速度は \(g = 9.8\,\rm m/s^2\) なので、空気抵抗がある場合と、ない場合での落下速度と落下距離をグラフにすると以下のようになる。


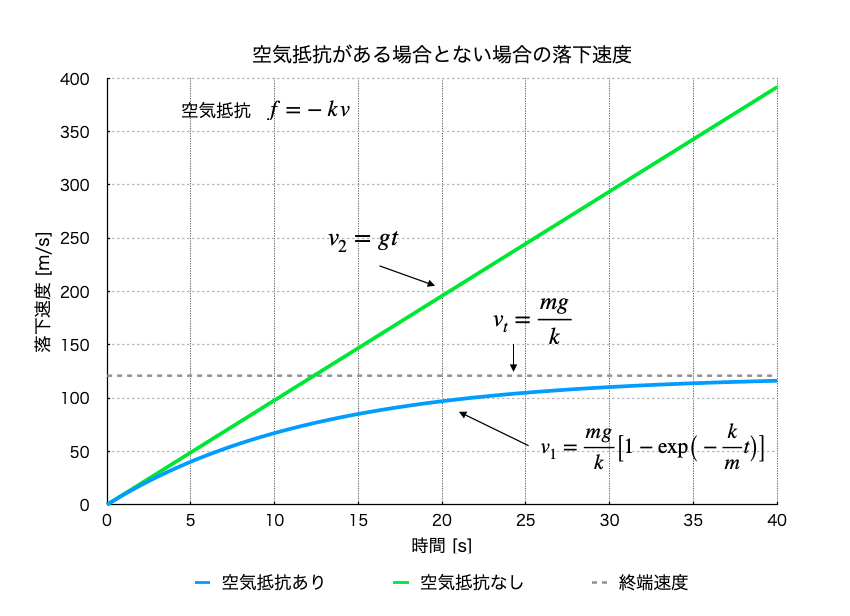
Fig.1　空気抵抗がある場合とない場合の落下速度


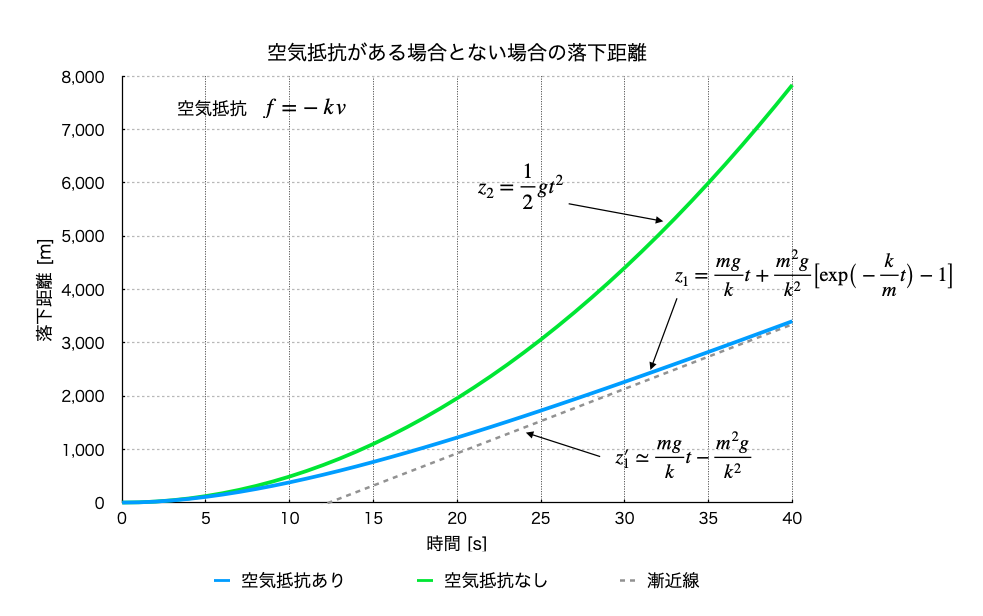
Fig.2　空気抵抗がある場合とない場合の落下距離

グラフから、速度に比例する空気抵抗が働いている場合は、落下速度は終端速度に近づいていき、落下距離も漸近線に近づいていっていることがわかる。では、この場合の終端速度はというと、
\begin{align} v_f\simeq 120\, \rm m/s\,(432 km/h) \end{align} となる。
ありゃ？ なんかやけに大きいなぁ。
時速 \(\rm 300\,km\) で走る新幹線でさえ秒速 \(\rm 83\,m\) なのに、秒速 \(\rm 120\,m\) は大きずぎる値だ。実際の雨粒の落下速度は秒速数 \(\rm m\) から \(10\,m\) 程度なので、その10倍以上の大きさだ。グラフから、この場合、\(\rm 2000\,m\) の高さから落下してくる雨粒が地上に達するまでの時間は \(27\) 秒ほどで、そのときの落下速度は \(110\,\rm m/s\) 弱なので、この段階ではまだ終端速度には達していないことがわかる。

ちなみに、雨粒の半径をもっと小さく \(a = 2 \times 10^{-4}\,\rm m\,(0.2\,mm)\) としてやると、終端速度は \(v_f \simeq 4.8\,\rm m/s\,(17.4\,km/h)\) と実際の値に近くなるので、この位小さな雨粒であれば、落下するときの空気抵抗は速度に比例すると考えられる。

では、半径 \(a = 1 \times 10^{-3}\,\rm m\,(1\,mm)\) ほどの大きさの雨粒の場合の空気抵抗はどのようになるのかというと、この場合は速度の2乗に比例すると考えられる。

Date: 2024/04/2920240429
Title: 一様な重力の中の運動：空気抵抗がある場合の落下運動(3)
Category: 物理
Keywords: 一様な重力、自由落下、空気抵抗

4. 速度の2乗に比例する空気抵抗があるの場合の自由落下①

前々回および前回の記事では、速度に比例する空気抵抗がある場合の落下運動について書いてきた。ここからは、空気抵抗が速度の2乗に比例する場合を考えてみよう。
この場合の空気抵抗は慣性抵抗と呼ばれ、質量 \(m\) の物体の運動方程式は鉛直下向きに \(z\) 軸をとると、
\begin{align} m\frac{dv}{dt}=mg-k'v^2 \end{align} ここで、\(k'/mg=\alpha^2\)（ただし、\(\alpha > 0\)）とおいて、上の方程式を変形すると、
\begin{align} \frac{dv}{dt}=g(1-\alpha^2v^2) \quad\quad\quad(5) \end{align} となる。これを解くには、まずは、これを変数分離するわけだが、
\begin{align} \frac{1}{1-\alpha^2v^2}=\frac{1}{2}\Big(\frac{1}{1-\alpha v}+\frac{1}{1+\alpha v}\Big) \end{align} なので、(5) 式は次のようになる。
\begin{align} \frac{1}{2}\Big(\frac{1}{1-\alpha v}+\frac{1}{1+\alpha v}\Big)dv=gdt \end{align} これを積分してやると、
\begin{align} & \frac{1}{2}\int\Big(\frac{1}{1-\alpha v}+\frac{1}{1+\alpha v}\Big)dv=g\int{}dt \\ & \\ \therefore\,-\ln{|1-\alpha v|} & +\ln{|1+\alpha v|}=2g\alpha t+2C\quad（C：積分定数）\quad(6) \end{align} さらにこれを変形すると、
\begin{align} & \ln{\biggl|\frac{1+\alpha v}{1-\alpha v}}\biggl|=2g\alpha t+2C \\ & \\ \therefore\,\biggl|\frac{1+\alpha v}{1-\alpha v}\biggl| & =\exp{[2(g\alpha t+C)]}=Be^{2g\alpha t}\,,\,(B=e^{2C})\quad\quad(7) \end{align} ここで、初期条件 \(t = 0\) のとき \(v = 0\) なので、\(B = 1\) 、つまり \(C = 0\) となる。
したがって、(7) 式は
\begin{align} \biggl|\frac{1+\alpha v}{1-\alpha v}\biggl|=e^{2g\alpha t} \quad\quad\quad(8) \end{align} となるが、ここからは (8) 式の分母が正負の場合に分けて考えていく。

1) 分母が正の場合：\(1 - \alpha v > 0,\,v > 0\) なので、\(0 < v < 1/\alpha\)
このとき、(8) 式は
\begin{align} \frac{1+\alpha v}{1-\alpha v}=e^{2g\alpha t} \end{align} となるので、
\begin{align} v=\frac{1}{\alpha}\frac{e^{2g\alpha t}-1}{1+e^{2g\alpha t}}=\frac{1}{\alpha}\frac{e^{g\alpha t}-e^{-g\alpha t}}{e^{g\alpha t}+e^{-g\alpha t}} \quad\quad\quad(9) \end{align} ん？　これはどこかでみたような関数だ。そう、双曲線関数だ（詳細は注 [1] を参照）。
したがって (9) 式は次のようになる。
\begin{align} v=\frac{1}{\alpha}\frac{\sinh{(g\alpha t)}}{\cosh{(g\alpha t)}}=\frac{1}{\alpha}\tanh{(g\alpha t)} \quad\quad\quad(10) \end{align}
2) (8) 式の分母が負の場合：\(1 - \alpha v < 0\) なので \(v > 1/\alpha\)
このとき同様に (8) 式を解くと以下のようになる。
\begin{align} v=\frac{1}{\alpha}\frac{e^{g\alpha t}+e^{-g\alpha t}}{e^{g\alpha t}-e^{g\alpha t}}=\frac{1}{\alpha}\coth{(g\alpha t)} \quad\quad\quad(11) \end{align} ここで、注 [1] のグラフから、式(10)、(11) をみてみると、(11)式 は \(t \rightarrow 0\) で発散するので、有意な解は
\begin{align} v=\frac{1}{\alpha}\tanh{(g\alpha t)} \quad\quad\quad(12) \end{align} であることがわかる。そこで、最初に \(k'/mg=\alpha^2\) とおいてやったので、\(\alpha = (k'/mg)^{1/2}\) を代入すると、(12) 式は
\begin{align} v=\sqrt{\frac{mg}{k'}}\tanh{\sqrt{\frac{k'g}{m}}t} \quad\quad\quad(13) \end{align} となる。この解は、初速度 \(v = 0\) で落下が始まり、\(t \rightarrow \infty\) で終端速度
\begin{align} v_t=\sqrt{\frac{mg}{k'}} \quad\quad\quad(14) \end{align} に近づいていくことを示している。

次に、(12) 式の積分を考える。
まず、\(f(t) = \cosh{(g\alpha t)}\) とおくと、\(f'(t) = g\alpha \sinh{(g\alpha t)}\) なので（注 [2] 参照） 、
\begin{align} v=\frac{1}{\alpha}\frac{\sinh{(g\alpha t)}}{\cosh{(g\alpha t)}}=\frac{1}{g\alpha^2}\frac{f'(t)}{f(t)} \end{align} これを使うと、(12) 式の積分は（注 [2] 参照）
\begin{align} z & = \int{v}dt=\frac{1}{g\alpha^2}\int{\frac{f'(t)}{f(t)}}dt \\ & =\frac{1}{g\alpha^2}\ln{(f(t))}+D \\ & =\frac{1}{g\alpha^2}\ln{(\cosh{(g\alpha t))}}+D \end{align} ここで、初期条件 \(t = 0\) のとき \(z = 0\) なので、\(D = 0\) 。したがって、
\begin{align} z=\frac{1}{g\alpha^2}\ln{(\cosh{(g\alpha t))}} \end{align} ここで、\(k'/mg=\alpha^2\) なので、 \begin{align} z=\frac{m}{k'}\ln{(\cosh{\sqrt{\frac{k'g}{m}}t})} \quad\quad\quad(15) \end{align} となる。
この式は、\(t \rightarrow \infty\) では、傾き \((mg/k')^{1/2}\)（終端速度）の直線に近づいていく。つまり、等速直線運動に近づいていくことを示している（注 [3] を参照）。

---

（注）
[1] 双曲線関数は指数関数 \(e^x\) を用いて次のように表される。
\begin{align} \sinh{x}=\frac{e^x-e^{-x}}{2}\,,\quad \cosh{x}=\frac{e^x+e^{-x}}{2}\,,\quad \tanh{x}=\frac{\sinh{x}}{\cosh{x}} \end{align} そこで、双曲線関数のグラフを描いてみると、以下のようになる。


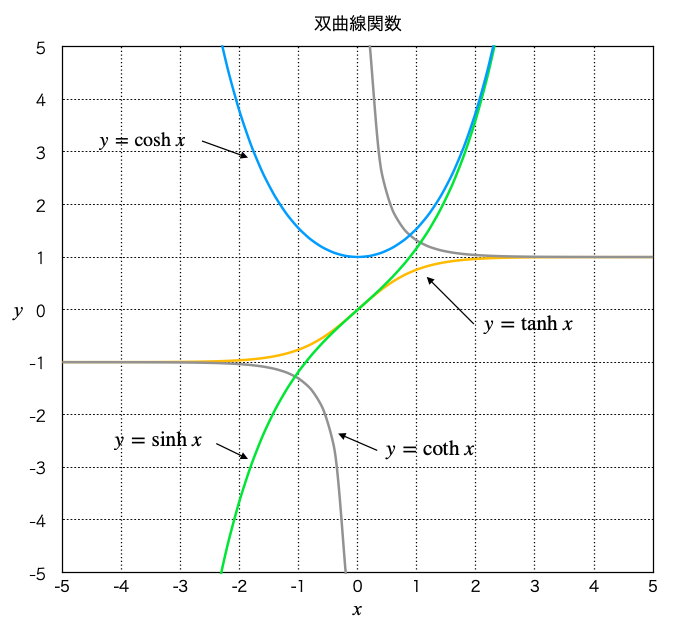
Fig 3　双曲線関数のグラフ

図の青い線、緑の線、オレンジの線、グレーの線がそれぞれ
\begin{align} & y=\cosh{x}=(e^x+e^{-x})/2\,\cdot\cdot\cdot\,\rm blue \\ & y=\sinh{x}=(e^x-e^{-x})/2\,\cdot\cdot\cdot\,\rm green \\ & y=\tanh{x}=\sinh{x}/\cosh{x}\,\cdot\cdot\cdot\,\rm orange \\ & y=\coth{x}=\cosh{x}/\sinh{x}\,\cdot\cdot\cdot\,\rm gray \end{align} を表している。

このグラフから、\(t \rightarrow \infty\) のとき、\(\tanh{(x)} \rightarrow 1\) に収束するのがわかる。 同様に、\(t \rightarrow 0\) のとき、\(\coth{(x)}\) は発散することがわかる。

[2] 双曲線関数の微分公式
\begin{align} \frac{d}{dx}\sinh{x}=\cosh{x}\,,\quad \frac{d}{dx}\cosh{x}=\sinh{x} \end{align} 対数関数の微分
\begin{align} \frac{d}{dx}\ln{[f(x)]}=\frac{f'(x)}{f(x)} \end{align} [3] 双曲線関数、対数、およびこれらを組み合わせた関数のグラフは次のようになる。


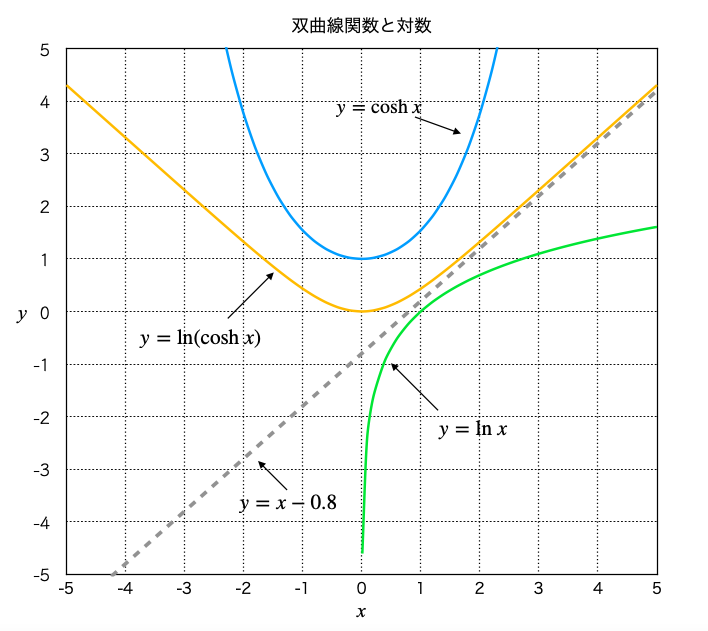
Fig.4　双曲線関数、対数、およびこれらを組み合わせた関数のグラフ

図の青い線、緑の線、オレンジの線はそれぞれ
\begin{align} & y=\cosh{x}\,\cdot\cdot\cdot\,\rm blue \\ & y=\ln{x}\,\cdot\cdot\cdot\,\rm green \\ & y=\ln{(\cosh{x})}\,\cdot\cdot\cdot\,\rm orange \end{align} を表している。図の黒い点線は \(y = x - 0.8\) の直線を表しているが、\(x \rightarrow \infty\) のとき、\(y = \ln{(\cosh{x})}\) は傾き 1 の直線（黒い点線）に近づいていっているのがわかる。
※黒い点線 \(y = x - 0.8\) の切片 \(0.8\) は、\(y = \ln{(\cosh{x})}\) が傾き 1 の直線に近づくのを示すために適当にとった。

Date: 2024/06/2920240629
Title: 一様な重力の中の運動：空気抵抗がある場合の落下運動(4)
Category: 物理
Keywords: 一様な重力、自由落下、空気抵抗

5. 速度の2乗に比例する空気抵抗があるの場合の自由落下②

前回は空気抵抗が速度の2乗に比例する場合の物体の落下運動について書いたが、そのつづきを書いていなかった。あれから何ヶ月が経っているので、思い出す意味でも改めて書いてみると、質量 \(m\) の物体の運動方程式は鉛直下向きに \(z\) 軸をとると次のようになる。
\begin{align} m\frac{dv}{dt}=mg-k'v^2 \end{align} その解は、
\begin{align} v=\sqrt{\frac{mg}{k'}}\tanh{\sqrt{\frac{k'g}{m}}t} \end{align} で、終端速度は
\begin{align} v_t=\sqrt{\frac{mg}{k'}} \end{align} となる。

さて、ここからが今回の本題だが、速度の2乗に比例する抵抗係数 \(k'\) は一般的に
\begin{align} k'=\frac{1}{2}C_D \rho_0 S \end{align} で表される。
ここで、\(C_D\) は物体の形状に依存する抗力係数で、球体の場合は \(C_D\sim0.5\) 程度の値となる。
\(\rho_0\) は流体の密度で、空気の場合は大体 \(\rho_0 = 1.2\,\rm kg/m^3\) という値だ。
\(S\) は落下する物体の断面積で、半径 \(a\) の雨粒では \(S = \pi a^2\) だ。
また、水の密度を \(\rho\,(\rho = 1.0 × 10^3\,\rm kg/m^3)\) とすると雨粒の質量は \(m = (4/3)\pi a^3 \rho\) なので、終端速度は
\begin{align} v_t=\sqrt{\frac{mg}{k'}} = \sqrt{\frac{8a \rho g}{3C_D \rho_0}} \end{align} となる。
具体的な数値を当てはめると、半径 \(a = 1\,\rm mm\) の雨粒の場合、\(v_t = 6.6\,\rm m/s\) となる。これは妥当な値と言える。
さらに、\(a = 2,\,5,\,10\,\rm mm\) の場合はそれぞれ \(v_t = 9.3,\,14.8,\,20.9\,\rm m/s\) となるので、半径 \(\rm 10\,mm\) の雨粒でも耐えられそうだ。ただし、大きな雨粒（文献によると、\(a > 3\,\rm mm\) [2]）は空気抵抗が大きくなって形が不安定となって、より小さな雨粒に分裂して降ってくるので、今回のような固体球モデルで雨粒を近似できるのは半径 \(\rm 1\,mm\) 程度が限界のようだ。

最後に、空気抵抗がない場合と、空気抵抗が速度に比例する場合と、速度の2乗に比例する場合の半径 \(a = 1\,\rm mm\) の雨粒の落下速度をグラフにすると以下のようになる。


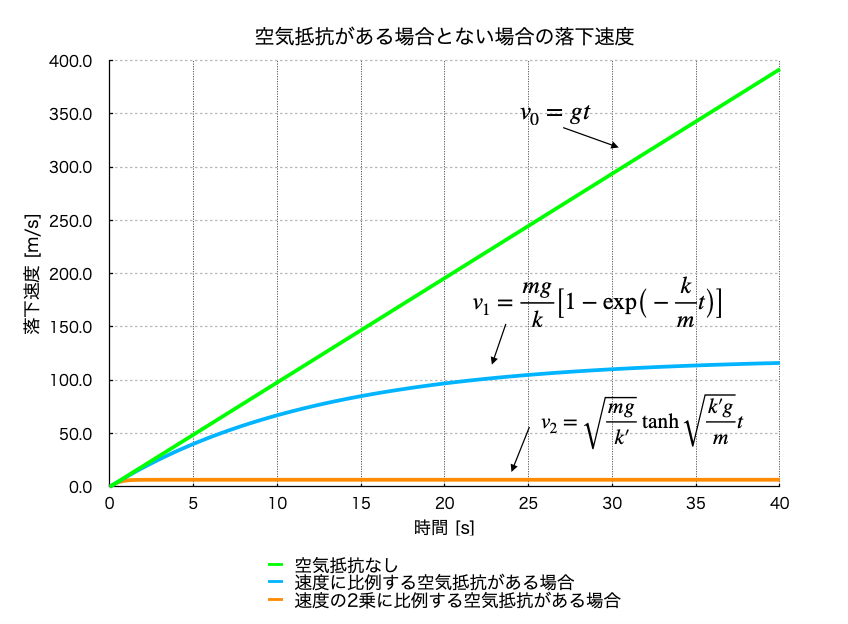
Fig.5　空気抵抗がある場合とない場合の雨粒の落下速度(1)（雨粒の半径 \(a=1\,\rm mm\)）

グラフから、空気抵抗が速度に比例する場合は終端速度に達するのに40秒以上かかるが、空気抵抗が速度の2乗に比例する場合はすぐに終端速度に達するのがわかる。しかし、少しわかりにくいので最初の5秒分を拡大すると以下のグラフのようになる。

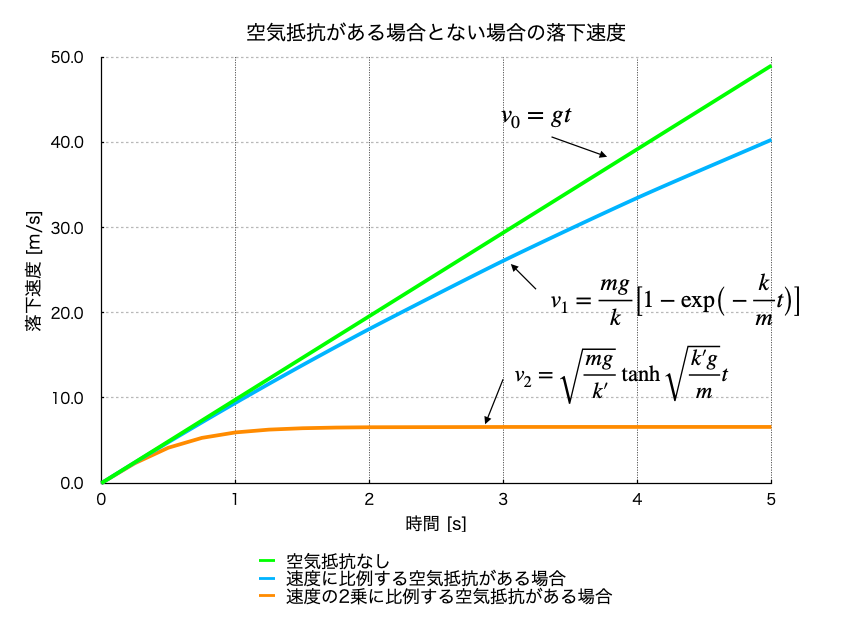
Fig.6　空気抵抗がある場合とない場合の雨粒の落下速度(2)（雨粒の半径 \(a=1\,\rm mm\)）

このグラフから空気抵抗が速度の2乗に比例する場合は2秒ほどで終端速度に達するのがわかる。


＜参考文献＞
[1] 増井、片岡、中村、常田、松山「高校物理における空気抵抗の正しい理解 ―風洞実験、理論解析、落下事件とデータ解析を通して―」
[2] 大庭、舟田「大気の抵抗があるときの固体球の落下運動」沼津工業高等専門学校研究報告 25, 第51号，2017年1月